题目内容
19.若方程$\frac{1}{x-2}+m=\frac{1-x}{2-x}$有增根,那么增根是x=2,m=1.分析 根据分式方程,可先进行化简,增根就是使得原分式方程无意义的根,从而可以解答本题.
解答 解:∵$\frac{1}{x-2}+m=\frac{1-x}{2-x}$,
∴$\frac{1+m(x-2)}{x-2}=\frac{x-1}{x-2}$.
化简得,
$\frac{mx-2m+1}{x-2}=\frac{x-1}{x-2}$.
∴mx-2m+1=x-1.
∴m=1,-2m+1=-1.
方程$\frac{1}{x-2}+m=\frac{1-x}{2-x}$的增根为x-2=0,得x=2.
故答案为:x=2,1.
点评 本题考查了分式方程的增根,解题的关键是先对分式方程化简,注意方程两边的对应量相等.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.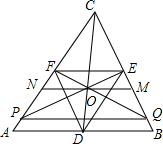 如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
 如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
如图,设D,E及F分别是△ABC的边AB,BC及CA的中点,∠BDC及∠ADC的角平分线分别交BC及AC于点M,N,直线MN交CD于点O.设EO及FO分别交AC及BC于点P及Q,求证:CD=PQ.
14.y=x-2的大致图象是( )
| A. |  | B. |  | C. |  | D. |  |
1.下列根式中,不能再化简的二次根式是( )
| A. | $\sqrt{{a^2}+1}$ | B. | -$\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{27}$ |
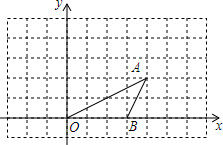 在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.
在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点. 已知 a、b、c三数在数轴上的位置如图所示,其中|a|=|c|,化简:$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+|c|-|a|.
已知 a、b、c三数在数轴上的位置如图所示,其中|a|=|c|,化简:$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|c|}{c}$+|c|-|a|.