题目内容
【题目】已知顶点为A的抛物线y=a(x- ![]() )2-2经过点B(-
)2-2经过点B(- ![]() ,2),点C(
,2),点C(![]() ,2).
,2).
(1)求抛物线的解析式;
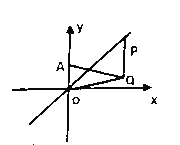
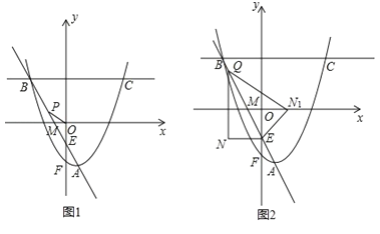
(2)如图1,直线AB与x轴相交于点M,与y轴相交于点E,抛物线与y轴相交于点F,在直线AB上有一点P,若∠OPM=∠MAF,求△POE的面积;
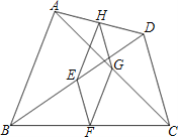
(3)如图2,点Q是折线A﹣B﹣C上一点,过点Q作QN∥y轴,过点E作EN∥x轴,直线QN与直线EN相交于点N,连接QE,将△QEN沿QE翻折得到△QEN1,若点N1落在x轴上,请直接写出Q点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)点Q的坐标为
;(3)点Q的坐标为![]() 或(
或(![]() )或(
)或(![]() ).
).
【解析】
(1)把点B(- ![]() ,2)代入
,2)代入![]() ,求得 a的值即可;
,求得 a的值即可;
(2)由已知可求得直线AB的解析式为:y=-2x-1,根据解析式易求E(0,-1), F(0, ![]() ),M(
),M(![]() ,0) ,由△OPE∽△FAE,继而求得OP的长,设点P(t,-2t-1),可得关于t的方程,解方程求得t的值,根据对称性可知方程的解都满足条件,由此即可得;
,0) ,由△OPE∽△FAE,继而求得OP的长,设点P(t,-2t-1),可得关于t的方程,解方程求得t的值,根据对称性可知方程的解都满足条件,由此即可得;
(3)若Q在AB上,点Q在BC上,且Q在y轴左侧,Q在BC上,且Q在y轴右侧,三种情况分别讨论即可得.
(1)把点B(- ![]() ,2)代入
,2)代入![]() ,解得 a=1
,解得 a=1
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ,
,
即![]() ;
;
(2)由(1)可得点A的坐标为(![]() ,-2)
,-2)
设直线AB解析式为:y=kx+b,代入点A,B的坐标得:
,解得:![]()
![]() 直线AB的解析式为:y=-2x-1
直线AB的解析式为:y=-2x-1
易求得E(0,-1), F(0, ![]() ),M(
),M(![]() ,0),
,0),
若∠OPM=∠MAF,
当OP∥AF时,则有△OPE∽△FAE
![]()
![]() ,
,
![]()
![]() ,
,
设点P(t,-2t-1),则![]()
解得: ![]()
由对称性知;当![]() 时,也满足∠OPM=∠MAF,
时,也满足∠OPM=∠MAF,
![]()
![]() 都满足条件,
都满足条件,
![]() △POE的面积=
△POE的面积=![]() ,
,
![]() △POE的面积为
△POE的面积为![]() 或
或![]() ;
;
(3)若Q在AB上运动,如图:设Q(a,-2a-1),则QN=-2a,NE=-a, ![]() =-2a
=-2a
易知△![]() ∽△
∽△![]() ,
,
![]()
![]()
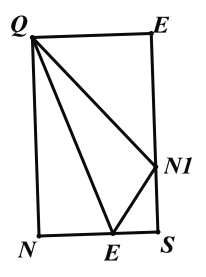
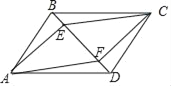
若Q在BC上运动,且Q在y轴左侧,如图:NE=a, ![]() ,
,
易知:![]()
![]()
Rt△![]() 中,
中, ![]()
![]() ;
;
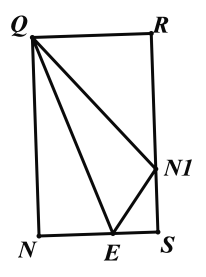
若Q在BC上运动,且Q在y轴右侧,如图:NE=a, ![]() ,
,
易知:![]()
![]()
Rt△![]() 中,
中, ![]()
![]() ;
;

综上所述Q点的坐标为:![]() .
.

 阅读快车系列答案
阅读快车系列答案