题目内容
 如图,E在AB上,F在DC上,G是BC延长线上的一点;
如图,E在AB上,F在DC上,G是BC延长线上的一点;(1)由∠B=∠1,可判断直线
(2)由∠1=∠D,可判断直线
(3)由∠A+∠D=180°,可判断直线
(4)由AD∥BC,EF∥BC,可判断直线
考点:平行线的判定
专题:
分析:(1)∠B和∠1是AB、CD被直线BC所截得到的一对同位角,可判定AB∥CD;
(2)∠1和∠D是AD、BC被直线DC所截得到的一对内错角,可判定AD∥BC;
(3)∠A和∠D是AB、CD补直线AD所截得到的一对同旁内角,可判定AB∥CD;
(4)由平行公理的推论,可判定AD∥EF.
(2)∠1和∠D是AD、BC被直线DC所截得到的一对内错角,可判定AD∥BC;
(3)∠A和∠D是AB、CD补直线AD所截得到的一对同旁内角,可判定AB∥CD;
(4)由平行公理的推论,可判定AD∥EF.
解答:解:
(1)∵∠B=∠1,
∴AB∥CD(同位角相等,两直线平行);
故答案为:AB;CD;同位角相等,两直线平行;
(2)∵∠1=∠D,
∴AD∥BC(内错角相等,两直线平行);
故答案为:AD;BC;内错角相等,两直线平行;
(3)∵∠A+∠D=180°,
∴AB∥CD(同旁内角互补,两直线平行);
故答案为:AB;CD;同旁内角互补,两直线平行;
(4)∵AD∥BC,EF∥BC,
∴AD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
故答案为:AD;EF;如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
(1)∵∠B=∠1,
∴AB∥CD(同位角相等,两直线平行);
故答案为:AB;CD;同位角相等,两直线平行;
(2)∵∠1=∠D,
∴AD∥BC(内错角相等,两直线平行);
故答案为:AD;BC;内错角相等,两直线平行;
(3)∵∠A+∠D=180°,
∴AB∥CD(同旁内角互补,两直线平行);
故答案为:AB;CD;同旁内角互补,两直线平行;
(4)∵AD∥BC,EF∥BC,
∴AD∥EF(如果两条直线都和第三条直线平行,那么这两条直线也互相平行),
故答案为:AD;EF;如果两条直线都和第三条直线平行,那么这两条直线也互相平行.
点评:本题主要考查平行线的判定,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c?a∥c.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
 如图,在正方形网格中,将△ABC顺时针旋转后得到△A′B′C′,则下列4个点中能作为旋转中心的是( )
如图,在正方形网格中,将△ABC顺时针旋转后得到△A′B′C′,则下列4个点中能作为旋转中心的是( )| A、点P | B、点Q | C、点R | D、点S |

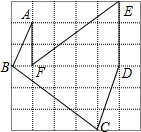 如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示
如图,这是由36个边长为1的小正方形拼成的方格图,依次连接小正方形的顶点A,B,C,D,E,F得线段AB,BC,CD,DE,EF,FA,请说出这些线段中的长度是有理数的有哪些,是无理数的有哪些,并在数轴上作出表示 在△ABC中,AB=30,AC=25,BC边上的高AD=18,求BC的长.
在△ABC中,AB=30,AC=25,BC边上的高AD=18,求BC的长. 如图,∠B=90°,AB=16cm,BC=12cm,AD=21cm,CD=29cm,求图(甲)凸四边形ABCD的面积?把图(甲)改成图(乙)凹四边形ABCD,求图(乙)凹四边形ABCD面积?
如图,∠B=90°,AB=16cm,BC=12cm,AD=21cm,CD=29cm,求图(甲)凸四边形ABCD的面积?把图(甲)改成图(乙)凹四边形ABCD,求图(乙)凹四边形ABCD面积? 如图,在△ABC中,AF平分∠BAC,BD⊥AF,BD交AF的延长线于点D,点E在AB上,且ED∥AC,
如图,在△ABC中,AF平分∠BAC,BD⊥AF,BD交AF的延长线于点D,点E在AB上,且ED∥AC,