题目内容
20．函数y=x+m与y=$\frac{m}{x}$（m≠0）在同一坐标系内的图象可以是（ ）| A． |  | B． |  | C． |  | D． |  |
分析 由一次函数系数k=1＞0，可得出一次函数在其定义域内单调递增，由此可排除B、D选项，再根据函数图象分析A、C选项中得m的取值范围，即可得出结论．
解答 解：∵一次函数y=x+m中k=1＞0，
∴一次函数图象单调递增，
∴B、D选项不合适；
A、一次函数图象过第一、三、四象限，m＜0；
反比例函数图象在第一、三象限，m＞0．
∴A不合适；
C、一次函数图象过第一、二、三象限，m＞0；
反比例函数图象在第一、三象限，m＞0．
∴C合适；
故选C．
点评 本题考查了反比例函数图象以及一次函数图象，解题的关键是根据函数的图象找出m的取值范围．本题属于基础题，难度不大，解决该题型题目时，根据函数图象经过的象限得出函数的系数的正负是关键．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
10．某工厂分发年终奖金，具体金额和人数如下表所示，则下列对这组数据的说法中不正确的是（ ）
| 人 数 | 1 | 3 | 5 | 70 | 10 | 8 | 3 |
| 金额（元） | 200000 | 150000 | 80000 | 15000 | 10000 | 8000 | 5000 |
| A． | 极差是195000 | B． | 中位数是15000 | C． | 众数是15000 | D． | 平均数是15000 |
11．某商品的进货成本为每件200元，促销期间，这种商品按原售价的8折出售，此时每卖出一件这种商品，只能获得10%的利润，设这种商品的原来售价是x元，所列方程正确的是（ ）
| A． | $\frac{0.8x-200}{200}$×100%=10% | B． | $\frac{200-0.8x}{200}$×100%=10% | ||
| C． | $\frac{0.8x-200}{x}$×100%=10% | D． | $\frac{200-0.8x}{x}$×100%=10% |
9．若正比例函数y=2x的图象经过点A（m，3m+1），则m的值为（ ）
| A． | 1 | B． | -1 | C． | $\frac{2}{5}$ | D． | -$\frac{2}{5}$ |
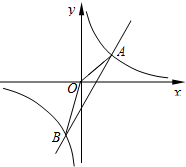如图，已知反比例函数y1=$\frac{{k}_{1}}{x}$的图象与一次函数y2=k2x+b的图象交于A、B两点，A（2，n），B（-$\frac{1}{2}$，-2）．