题目内容
9.若△ABC三边的长分别为$\sqrt{{m}^{2}+16{n}^{2}}$、$\sqrt{9{m}^{2}+4{n}^{2}}$、2$\sqrt{{m}^{2}+{n}^{2}}$(m>0,n>0.且m≠n).试运用构图法求出这三角形的面积.分析 由题意得出此三角形的三边分别是直角边长为m,4n的直角三角形的斜边;直角边长为3m,2n的直角三角形的斜边;直角边长为2m,2n的直角三角形的斜边.同样把它整理为一个矩形的面积减去三个直角三角形的面积,即可得出结果.
解答 解:由勾股定理得:$\sqrt{{m}^{2}+(4n)^{2}}$=$\sqrt{{m}^{2}+16{n}^{2}}$,$\sqrt{(3m)^{2}+(2n)^{2}}$=$\sqrt{9{m}^{2}+4{n}^{2}}$,$\sqrt{(2m)^{2}+(2n)^{2}}$=2$\sqrt{{m}^{2}+{n}^{2}}$,
构造△ABC所示,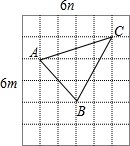 S△ABC=3m×4n-$\frac{1}{2}$×m×4n-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×2m×2n=5mn.
S△ABC=3m×4n-$\frac{1}{2}$×m×4n-$\frac{1}{2}$×3m×2n-$\frac{1}{2}$×2m×2n=5mn.
点评 本题考查了勾股定理、三角形面积的计算方法;关键是结合网格用矩形及容易求得面积的直角三角形表示出所求三角形的面积进行解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.下列变形不正确的是( )
| A. | (3x3-5)(3x3+5)=9x6-25 | B. | (a+b+c+d)(a+b-c-d)=(a+b)2-(c+d)2 | ||
| C. | 50$\frac{1}{3}$×49$\frac{2}{3}$=502-($\frac{1}{3}$)2 | D. | 2(2a-b)2(4a+2b)2=(16a2-4b2)2 |
 如图,某小区宿舍楼甲楼坐落在正南正北方向,高16m,现在在甲楼后盖座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼6m,若甲楼的影子刚好不影响乙楼的采光,两楼距离应是多少m?
如图,某小区宿舍楼甲楼坐落在正南正北方向,高16m,现在在甲楼后盖座乙楼,冬天太阳最低时的正午时刻,若两楼相距20m,则甲楼的影子将落在乙楼6m,若甲楼的影子刚好不影响乙楼的采光,两楼距离应是多少m? 如图所示,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AB,PF⊥AC,BD是AC边上的高,试探究PE+PF与BD之间的数量关系.
如图所示,在△ABC中,AB=AC,P是BC边上的一点,PE⊥AB,PF⊥AC,BD是AC边上的高,试探究PE+PF与BD之间的数量关系.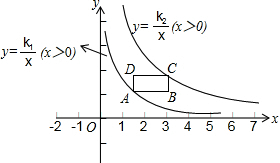 如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,点C在反比例函数L2:y=$\frac{{k}_{2}}{x}$(x>0)的图象上.
如图,在平面直角坐标系的第一象限中,有一各边所在直线均平行于坐标轴的矩形ABCD,且点A在反比例函数L1:y=$\frac{{k}_{1}}{x}$(x>0)的图象上,点C在反比例函数L2:y=$\frac{{k}_{2}}{x}$(x>0)的图象上.