题目内容
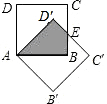 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是分析:连接D′C,根据旋转的性质及正方形的性质分别求得△ABC与△CD′E的面积,从而不难求得重叠部分的面积.
解答: 解:连接D′C,
解:连接D′C,
∵绕顶点A顺时针旋转45°,
∴∠D′CE=45°,
∵ED′⊥AC,
∴∠CD′E=90°,
∵AC=
=
,
∴CD′=
-1,
∴正方形重叠部分的面积是
×1×1-
×(
-1)(
-1)=
-1.
 解:连接D′C,
解:连接D′C,∵绕顶点A顺时针旋转45°,
∴∠D′CE=45°,
∵ED′⊥AC,
∴∠CD′E=90°,
∵AC=
| 12+12 |
| 2 |
∴CD′=
| 2 |
∴正方形重叠部分的面积是
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
点评:解答此题,要找出题中的隐含条件,构造出等腰直角三角形解答.

练习册系列答案
相关题目
 附加题
附加题
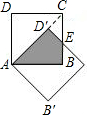
 如图,边长为3的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是多少?
如图,边长为3的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是多少? 如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是( )
如图.边长为1的两个正方形互相重合,按住其中一个不动,将另一个绕顶点A顺时针旋转45°,则这两个正方形重叠部分的面积是( ) 如图,边长为3的两个正方形重合在一起,将其中一个固定不动,另一个绕顶点A旋转45°,求这两个正方形重合部分的面积.
如图,边长为3的两个正方形重合在一起,将其中一个固定不动,另一个绕顶点A旋转45°,求这两个正方形重合部分的面积. 如图,边长为4的两个正方形,则阴影部分的面积为
如图,边长为4的两个正方形,则阴影部分的面积为