题目内容
5．计算：|-7|-（1-π）0+（$\frac{1}{3}$）-1．分析 直接利用绝对值的性质以及零指数幂的性质和负整数指数幂的性质分别化简求出答案．
解答 解：原式=7-1+3
=9．
点评 本题主要考查了实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟练掌握零指数幂、负整数指数幂的性质、绝对值等考点的运算．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
15．要使$\sqrt{x-1}$有意义，则x的取值范围是（ ）
| A． | x＜1 | B． | x≥1 | C． | x≤-1 | D． | x＜-1 |
已知：如图，在△AOB中，∠AOB=90°，AO=3cm，BO=4cm．将△AOB绕顶点O，按顺时针方向旋转到△A1OB1处，此时线段OB1与AB的交点D恰好为AB的中点，则线段B1D=1.5cm．
20．
如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S△ABF=S△ADF；②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是（ ）
如图，已知正方形ABCD，点E是BC边的中点，DE与AC相交于点F，连接BF，下列结论：①S△ABF=S△ADF；②S△CDF=4S△CEF；③S△ADF=2S△CEF；④S△ADF=2S△CDF，其中正确的是（ ）| A． | ①③ | B． | ②③ | C． | ①④ | D． | ②④ |
10．
如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE=$\sqrt{5}$，∠EAF=135°，则以下结论正确的是（ ）
如图，四边形ABCD是边长为1的正方形，E，F为BD所在直线上的两点．若AE=$\sqrt{5}$，∠EAF=135°，则以下结论正确的是（ ）| A． | DE=1 | B． | tan∠AFO=$\frac{1}{3}$ | ||
| C． | AF=$\frac{\sqrt{10}}{2}$ | D． | 四边形AFCE的面积为$\frac{9}{4}$ |
3．$\frac{4}{9}$的分子加上12，要使原分数大小不变，分母应加上…（ ）
| A． | 12 | B． | 27 | C． | 36 | D． | 45 |
20．
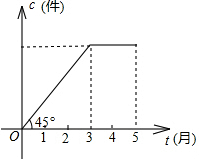某村办工厂2016年前五个月生产某种产品的总量c（万件）与时间t（月）的函数图象如图所示，则该厂对这种产品来说（ ）
某村办工厂2016年前五个月生产某种产品的总量c（万件）与时间t（月）的函数图象如图所示，则该厂对这种产品来说（ ）| A． | 1月至3月每月生产总量逐月增加，4、5两月每月生产总量逐月减少 | |
| B． | 1月至3月每月生产总量逐月增加，4、5两月生产总量与3月持平 | |
| C． | 1月至3月每月生产总量不变，4、5两月均停止生产 | |
| D． | 1月至3月每月生产总量逐月增加，4、5两月均停止生产 |