题目内容
1．在函数y=$\frac{2}{x}$的图象上有A（1，y1）、B（-1，y2）、C（-2，y3）三个点，则y1，y2与y3的大小关系为y2＜y3＜y1．分析 根据反比例函数的增减性解答即可．
解答 
解：∵k＞0，函数图象如图，
∴图象在第一、三象限，在每个象限内，y随x的增大而减小，
∵-2＜-1＜1，
∴y2＜y3＜y1．
故答案为y2＜y3＜y1．
点评 本题考查的是反比例函数图象上点的坐标特点，由反比例函数的图象确定y2，y1，y3的关系．
练习册系列答案
名校课堂系列答案
相关题目
如图，直线AB、CD相交与点O，OE是∠AOD的平分线，∠AOC=26°，求：
12．在半径为R的圆中，它的内接正三角形、内接正方形、内接正六边形的边长之比为（ ）
| A． | 1：$\sqrt{2}$：$\sqrt{3}$ | B． | $\sqrt{3}$：$\sqrt{2}$：1 | C． | 1：2：3 | D． | 3：2：1 |
16．
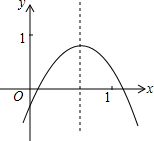二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的是（ ）
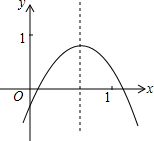二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论正确的是（ ）| A． | a＞0 | B． | abc＞0 | C． | a+b+c＜0 | D． | b2-4ac＜0 |
如图是正方体的展开图，则正方体中与数字5所在面相对的面上的数字为4．
如图，沿所画线折叠能形成一个立体图形，它的名称是三棱柱．