题目内容
9.规定:logab(a>0,a≠1,b>0)表示a,b之间的一种运算.现有如下的运算法则:logaan=n.logNM=$\frac{lo{g}_{n}M}{lo{g}_{n}N}$(a>0,a≠1,N>0,N≠1,M>0).
例如:log223=3,log25=$\frac{lo{g}_{10}5}{lo{g}_{10}2}$,则log1001000=$\frac{3}{2}$.
分析 先根据logNM=$\frac{lo{g}_{n}M}{lo{g}_{n}N}$(a>0,a≠1,N>0,N≠1,M>0)将所求式子化成以10为底的对数形式,再利用公式$lo{g}_{n}{n}^{a}=a$进行计算.
解答 解:先由公式logNM=$\frac{lo{g}_{n}M}{lo{g}_{n}N}$得:log1001000=$\frac{lo{g}_{10}1000}{lo{g}_{10}100}$,
由公式logaan=n得:①log101000=$lo{g}_{10}1{0}^{3}$=3;
②log10100=$lo{g}_{10}1{0}^{2}$=2;
∴log1001000=$\frac{lo{g}_{10}1000}{lo{g}_{10}100}$=$\frac{lo{g}_{10}1{0}^{3}}{lo{g}_{10}1{0}^{2}}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了实数的运算,这是一个新的定义,利用已知所给的新的公式进行计算.认真阅读,理解公式的真正意义;解决此类题的思路为:观察所求式子与公式的联系,发现1000与100都与10有关,且都能写成10的次方的形式,从而使问题得以解决.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.计算x4÷x+x3的结果是( )
| A. | x4 | B. | x3 | C. | 2x3 | D. | 2x4 |
14.观察图中正方形四个顶点所标的数字规律,可知,数2016应标在( )
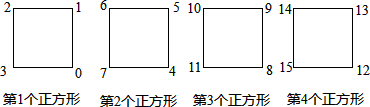

| A. | 第504个正方形的左下角 | B. | 第504个正方形的右下角 | ||
| C. | 第505个正方形的左上角 | D. | 第505个正方形的右下角 |
1.下列运算正确的是( )
| A. | a2+a3=a5 | B. | (a+2b)2=a2+2ab+b2 | C. | a6÷a3=a2 | D. | (-2a3)2=4a6 |
19.2016的倒数是( )
| A. | $\frac{1}{2016}$ | B. | -$\frac{1}{2016}$ | C. | 2016 | D. | -2016 |
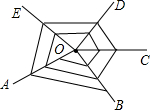 如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.
如图所示,以O为端点画5条射线OA,OB,OC,OD,OE后,再从射线OA上某点开始按逆时针方向依次在射线上描点并连线,若将各条射线所描的点依次记为1,2,3,4,5,6,7,8…后,那么所描的第2016个点在射线OA上.


 如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.
如图,直线l:y=-x+1与x轴,y轴分别交于A,B两点,点P,Q是直线l上的两个动点,且点P在第二象限,点Q在第四象限,∠POQ=135°.