题目内容
14.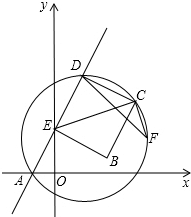 如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.
如图,直线y=2x+2与x轴,y轴分别交于A,E两点,D是第一象限内直线y=2x+2上运动的一个动点,以ED为边作正方形EDCB,连结CE,作EC⊥CF与过A,D,C三点的圆交于点F,连结DF.(1)求AE的长;
(2)请你在图中连结已标注字母的两点,从而构造一个三角形与△FDC相似,并说明理由.
(3)点D在运动过程中,CF的长度是否改变?若不变,请求出CF的长;若变化,请说明理由.
分析 (1)先确定E点坐标为(0,2),A点坐标为(-1,0),然后利用勾股定理计算AE;
(2)连结AC,先根据正方形的性质得∠DCE=∠DEC=45°,则∠AEC=135°,再计算出∠DCF=135°,则∠AEC=∠DCF,然后根据圆周角定理得∠DAC=∠DFC,
于是根据三角形相似的判定方法得到△ACE∽△FDC;
(3)由△ACE∽△FDC得到$\frac{AE}{CF}$=$\frac{EC}{DC}$,再根据△DEC为等腰直角三角形得到EC=$\sqrt{2}$DC,然后利用相似比可计算出CF=$\frac{\sqrt{10}}{2}$.
解答 解:(1)把x=0代入y=2x+2得y=2,则E点坐标为(0,2),
把y=0代入y=2x+2得2x+2=0,解得x=-1,则A点坐标为(-1,0),
所以AE=$\sqrt{O{A}^{2}+O{E}^{2}}$=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$;
(2)连结AC,则△ACE∽△FDC.理由如下:
∵四边形BEDC为正方形,
∴∠DCE=∠DEC=45°,
∴∠AEC=135°,
∵EC⊥CF,
∴∠DCF=45°+90°=135°,
∴∠AEC=∠DCF,
∵∠DAC=∠DFC,
∴△ACE∽△FDC;
(3)CF的长度不改变.
∵△ACE∽△FDC,
∴$\frac{AE}{CF}$=$\frac{EC}{DC}$,
∵△DEC为等腰直角三角形,
∴EC=$\sqrt{2}$DC,
∴$\frac{\sqrt{5}}{CF}$=$\sqrt{2}$,
∴CF=$\frac{\sqrt{10}}{2}$.
点评 本题考查了圆的综合题:熟练掌握圆周角定理和正方形的性质;会利用勾股定理和相似比进行几何计算.

练习册系列答案
相关题目
2.从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
根据以上数据可以估计,该玉米种子发芽的概率约为0.80(精确到0.10).
| 种子粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
| 发芽种子粒数 | 85 | 318 | 652 | 793 | 1604 | 4005 |
| 发芽频率 | 0.850 | 0.795 | 0.815 | 0.793 | 0.802 | 0.801 |
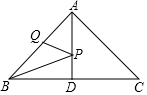 如图,在△ABC中,AB=AC=10,BC=12,AD是角平分线,P,Q分别是AD、AB上的动点,则BP+PQ的最小值为9.6.
如图,在△ABC中,AB=AC=10,BC=12,AD是角平分线,P,Q分别是AD、AB上的动点,则BP+PQ的最小值为9.6. 如图,⊙O为△ABC的外接圆,其中D点在$\widehat{AC}$上,且OD⊥AC,已知∠A=36°,∠C=60°,则∠BOD=156°.
如图,⊙O为△ABC的外接圆,其中D点在$\widehat{AC}$上,且OD⊥AC,已知∠A=36°,∠C=60°,则∠BOD=156°.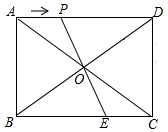 如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.
如图,在矩形ABCD中,AB=6cm,BC=8cm,对角线AC,BD交于点O,点P从点A出发,沿AD方向匀速运动,速度为2cm/s,当OD平分∠COP时,运动时间为$\frac{56}{39}$s.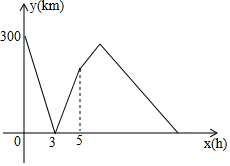 甲,乙两车分别从A,B两地同时相向匀速行驶,乙车到达A地后未作停留,继续保持原速向远离B地的方向行驶,而甲车到达B地后修整了1个小时,然后调头并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数图象如图所示,则A,C两地相距420千米.
甲,乙两车分别从A,B两地同时相向匀速行驶,乙车到达A地后未作停留,继续保持原速向远离B地的方向行驶,而甲车到达B地后修整了1个小时,然后调头并保持原速与乙车同向行驶,经过一段时间后两车同时到达C地.设两车行驶的时间为x(小时),两车之间的距离为y(千米),y与x之间的函数图象如图所示,则A,C两地相距420千米. 如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.