题目内容
 如图,△ABC是边长为a的等边三角形,D是BC边的中点,DE⊥AC于E,则CE的长为( )
如图,△ABC是边长为a的等边三角形,D是BC边的中点,DE⊥AC于E,则CE的长为( )A、
| ||
B、
| ||
C、
| ||
| D、a |
考点:等边三角形的性质,含30度角的直角三角形
专题:
分析:先根据△ABC是边长为a的等边三角形,D是BC边的中点得出CD的长∠C的度数,再根据DE⊥AC可知∠DEC=90°,故可得出∠EDC的度数,根据直角三角形的性质可得出CE的长.
解答:解:∵△ABC是边长为a的等边三角形,D是BC边的中点,
∴CD=
BC=
a,∠C=60°.
∵DE⊥AC,
∴∠DEC=90°,
∴∠EDC=30°,
∴CE=
CD=
BC=
a.
故选A.
∴CD=
| 1 |
| 2 |
| 1 |
| 2 |
∵DE⊥AC,
∴∠DEC=90°,
∴∠EDC=30°,
∴CE=
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
故选A.
点评:本题考查的是等边三角形的性质,熟知等边三角形的三个内角都相等,且都等于60°是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列说法中,正确的是( )
| A、生活中,如果一个事件不是不可能事件,那么它就必然发生 |
| B、生活中,如果一个事件可能发生,那么它就是必然事件 |
| C、生活中,如果一个事件发生的可能性很大,那么它也可能不发生 |
| D、生活中,如果一个事件不是必然事件,那么它就不可能发生 |
我市某中学九年级一班准备组织参加旅游,班长把全班48名同学对旅游地点的意向绘制成了扇形统计图,其中“想去海洋馆学生数”的扇形圆心角为60°,则下列说法中正确的是( )
| A、想去海洋馆的学生占全班学生的60% | ||
| B、想去海洋馆学生有12人 | ||
| C、想去海洋馆的学生肯定最多 | ||
D、想去海洋馆学生占全班学生的
|
 如图,D是∠BAC角平分线上异于A的一点,B、C分别是∠BAC两边上异于A的任意一点,连接DB和DC,分别增加下列条件后,仍不能判定△ADB≌△ADC的是( )
如图,D是∠BAC角平分线上异于A的一点,B、C分别是∠BAC两边上异于A的任意一点,连接DB和DC,分别增加下列条件后,仍不能判定△ADB≌△ADC的是( )| A、AB=AC |
| B、DC=DB |
| C、∠ACD=∠ABD |
| D、∠ADC=∠ADB |
 如图,双曲线y=
如图,双曲线y=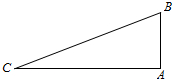 如图,在Rt△ABC中,AB=5,AC=12,∠A=90°.
如图,在Rt△ABC中,AB=5,AC=12,∠A=90°.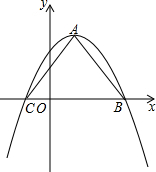 如图,在平面直角坐标系中,抛物线C1:y=-x2+2x+3的顶点为A,与x轴交于两点.
如图,在平面直角坐标系中,抛物线C1:y=-x2+2x+3的顶点为A,与x轴交于两点. 学校举行“歌手大赛”后将参加预赛选手的成绩(满分为100分,得分为整数,最低为80分,且无满分)分成四组,并绘制了如下的统计图,请根据统计图的信息解答下列问题.
学校举行“歌手大赛”后将参加预赛选手的成绩(满分为100分,得分为整数,最低为80分,且无满分)分成四组,并绘制了如下的统计图,请根据统计图的信息解答下列问题.