题目内容
小明用一根长为120cm的铁丝围成一个矩形
(1)若围成的矩形的面积为500cm2,矩形的长和宽分别是多少?
(2)小强对小明说:“这个矩形的面积不可能等于1000cm2,他的说法对吗?请说明理由.
(1)若围成的矩形的面积为500cm2,矩形的长和宽分别是多少?
(2)小强对小明说:“这个矩形的面积不可能等于1000cm2,他的说法对吗?请说明理由.
考点:一元二次方程的应用
专题:几何图形问题
分析:(1)设矩形的长为xcm,则宽为:(60-x)cm,利用长乘宽=矩形面积,进而求出即可;
(2)设矩形的长为xcm,则宽为:(60-x)cm,利用长乘宽=矩形面积,结合△的符号进而求出即可;
(2)设矩形的长为xcm,则宽为:(60-x)cm,利用长乘宽=矩形面积,结合△的符号进而求出即可;
解答:解:设矩形的长为xcm,则宽为(60-x)cm,
依题意得:x(60-x)=500,
解得:x=10或x=50,
∵x为矩形的长,
∴经检验x=10不合题意,舍去,
∴x=50
此时宽为(60-x)=60-50=10cm;
答:矩形的长和宽分别是50cm,10cm.
(2)他的说法对.如果有可能,则x(60-x)=1000
∴x2-60x+1000=0,
∵△=b2-4ac=(-60)2-4×1×1000=-400<0,
∴此时一元二次方程没有实数根,
∴这个矩形的面积不可能等于1000cm2,小强的说法对.
依题意得:x(60-x)=500,
解得:x=10或x=50,
∵x为矩形的长,
∴经检验x=10不合题意,舍去,
∴x=50
此时宽为(60-x)=60-50=10cm;
答:矩形的长和宽分别是50cm,10cm.
(2)他的说法对.如果有可能,则x(60-x)=1000
∴x2-60x+1000=0,
∵△=b2-4ac=(-60)2-4×1×1000=-400<0,
∴此时一元二次方程没有实数根,
∴这个矩形的面积不可能等于1000cm2,小强的说法对.
点评:此题主要考查了一元二次方程的应用以及根的判别式和二次函数最值求法,得出矩形面积与长乘宽的关系是解题关键.

练习册系列答案
相关题目
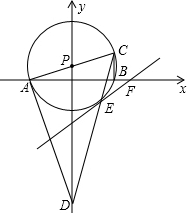 如图,已知P(0,1),⊙P与x轴交于A、B两点,AC是⊙P的直径,OA、OD的长是关于x的方程x2-3kx+2k2=0的两根,且OA2+OD2=20.
如图,已知P(0,1),⊙P与x轴交于A、B两点,AC是⊙P的直径,OA、OD的长是关于x的方程x2-3kx+2k2=0的两根,且OA2+OD2=20. 已知△ABC中,AB=AC,CD⊥AB于点D.
已知△ABC中,AB=AC,CD⊥AB于点D.