Question

18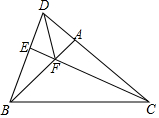．如图，△ABC中，AB=AC，∠BAC=90°，CE⊥DB，求∠DFB．

Answer 1

分析 先根据∠CED=∠CAF=90°、∠FAC=∠DCE可得∠CFA=∠CDE，再证△BAD≌△CAF得DA=FA，从而知△DAF为等腰直角三角形，即∠DFA=45°，继而得出答案．

解答 解：∵CE⊥DB，
∴∠CED=∠CAF=90°，
∵∠FAC=∠DCE，
∴∠CFA=∠CDE，
在△BAD和△CAF中，
∵$\left\{\begin{array}{l}{BA=CA}\\{∠BAD=∠CAF=90°}\\{∠BDA=∠CFA}\end{array}\right.$，
∴△BAD≌△CAF（AAS），
∴DA=FA，
又∵∠BAD=90°，
∴△DAF为等腰直角三角形，
∴∠DFA=45°，
∴∠DFB=135°．

点评 本题主要考查全等三角形的判定与性质、等腰直角三角形的判定与性质，通过证明△BAD≌△CAF得出DA=FA是解题的关键．