题目内容
第一盒中有2个白球、1个黄球,第二盒中有1个白球、1个黄球,这些球除颜色外无其他差别,分别从每个盒中随机取出1个球,求下列事件的概率:
(1)取出的2个球都是黄球;
(2)取出的2个球中1个白球、1个黄球.
(1)取出的2个球都是黄球;
(2)取出的2个球中1个白球、1个黄球.
考点:列表法与树状图法
专题:计算题
分析:(1)先画出树状图展示所有6种等可能的结果数,再找出2个球都是黄球所占结果数,然后根据概率公式求解;
(2)找出1个白球、1个黄球所占结果数,然后根据概率公式求解.
(2)找出1个白球、1个黄球所占结果数,然后根据概率公式求解.
解答:解:(1)画树状图为: ,
,
共有6种等可能的结果数,其中2个球都是黄球占1种,
所以取出的2个球都是黄球的概率=
;
(2)共有6种等可能的结果数,其中1个白球、1个黄球占3种可能,
所以取出的2个球中1个白球、1个黄球的概率=
=
.
 ,
,共有6种等可能的结果数,其中2个球都是黄球占1种,
所以取出的2个球都是黄球的概率=
| 1 |
| 6 |
(2)共有6种等可能的结果数,其中1个白球、1个黄球占3种可能,
所以取出的2个球中1个白球、1个黄球的概率=
| 3 |
| 6 |
| 1 |
| 2 |
点评:本题考查了列表法与树状图法:运用列表法或树状图法展示所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.

练习册系列答案
相关题目
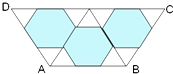 角进行清扫,改成一个小花坛,该等腰梯形上底角为60°,上底是下底的2倍,AB=6m,若按图案在三个正六边形中种上花圃.求:
角进行清扫,改成一个小花坛,该等腰梯形上底角为60°,上底是下底的2倍,AB=6m,若按图案在三个正六边形中种上花圃.求: