题目内容
1．若不等式$\left\{\begin{array}{l}x-a＞0\\ x＜a+1\end{array}\right.$的解集中任一个x的值均不在2≤x≤5的范围内，则a的取值范围是a≥5或a≤1．分析 根据解不等式组，可得不等式的解集，根据不等式的解集不在2≤x≤5，可得关于a的不等式，根据解不等式，可得答案．
解答 解：$\left\{\begin{array}{l}x-a＞0\\ x＜a+1\end{array}\right.$得a＜x＜a+1，
由不等式$\left\{\begin{array}{l}x-a＞0\\ x＜a+1\end{array}\right.$的解集中任一个x的值均不在2≤x≤5的范围内，得
a≥5或a+1≤2，
解得a≥5或a≤1，
故答案为：a≥5或a≤1．
点评 本题考查了不等式的解集，解答此题要根据不等式组解集的求法解答．求不等式组的解集，应注意：同大取较大，同小取较小，小大大小中间找，大大小小解不了．
练习册系列答案
相关题目
11．下列变形正确的是（ ）
| A． | $\sqrt{4\frac{9}{25}}$=$\sqrt{4}$×$\sqrt{\frac{9}{25}}$=2×$\sqrt{\frac{3}{5}}$=$\frac{6}{5}$ | B． | $\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{4{1}^{2}}$-$\sqrt{4{0}^{2}}$=41-40=1 | ||
| C． | 2$\sqrt{3}$×（-5$\sqrt{27}$）=-2×5×$\sqrt{3×27}$=-90 | D． | -3$\sqrt{2}$=$\sqrt{（-3）^{2}×2}$=$\sqrt{18}$ |
12．设M=（4+2$\sqrt{3}$）3，其小数部分为P，则M（1-P）=（ ）
| A． | 58 | B． | 64 | C． | 73 | D． | 82 |
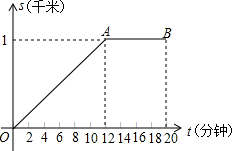小亮早晨从家里出发匀速步行去上学，小亮的妈妈在小亮出发后10分钟，发现小亮的数学课本没带，于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮，结果与小亮同时到达学校．已知小亮在整个上学途中，他出发后t分钟时，他所在的位置与家的距离为s千米，且s与t之间的函数关系的图象如图中的折线段OA-AB所示．
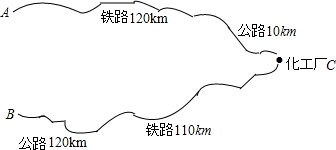如图，某化工厂C与A、B两地有公路、跌路相连．这家工厂从A地购买一批每吨1000元的原料回工厂，制成若干每吨8000元的产品运回B地．已知公路运价为1.5元/（吨．千米），铁路运价为1.2元/（吨．千米），若这两次运输共支出铁路运费97200元，且这批产品的销售款比原料费与运输费的和多1887800元．这两次运输共支出公路运输费多少元？
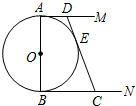如图，⊙O的直径AB=2，AM和BN是它的两条切线，DE切⊙O于E，交AM于D，交BN 于C．设AD=x，BC=y．