题目内容
18.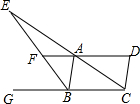 在?ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E.
在?ABCD中,∠ABC的外角∠ABG的平分线BE分别交DA,CA的延长线于点F、E.(1)求证:AB=AF;
(2)当AB=3,BC=5时,求$\frac{AE}{AC}$的值.
分析 (1)由平行四边形的性质得出DF∥BC,由平行线的性质得出∠AFB=∠FBG,再由角平分线证出∠ABF=∠AFB,即可得出结论;
(2)由平行线得出△EFA∽△EBC,得出对应边成比例$\frac{AE}{CE}=\frac{AF}{BC}=\frac{AB}{BC}$=$\frac{3}{5}$,再由比例的性质即可得出结果.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
∴DF∥BC,
∴∠AFB=∠FBG,
∵BF平分∠ABG,
∴∠ABF=∠FBG,
∴∠ABF=∠AFB,
∴AB=AF;
(2)解:∵FD∥CG,
∴△EFA∽△EBC,
∴$\frac{AE}{CE}=\frac{AF}{BC}=\frac{AB}{BC}$=$\frac{3}{5}$,
∴$\frac{AE}{AC}$=$\frac{3}{2}$.
点评 本题考查了平行四边形的性质、等腰三角形的判定、相似三角形的判定与性质、比例的性质;熟练掌握平行四边形的性质,证明AB=AF是解决问题的关键.

练习册系列答案
相关题目
6.一个黑色不透明的袋子里装有除颜色外其余都相同的7个红球和3个白球,那么从这个袋子中摸出一个红球的可能性和摸出一个白球的可能性相比( )
| A. | 摸出一个红球的可能性大 | B. | 摸出一个白球的可能性大 | ||
| C. | 两种可能性一样大 | D. | 无法确定 |
10.下列事件中,是必然事件的是( )
| A. | 明天一定会下雨 | B. | 购买一张彩票,中奖 | ||
| C. | 抛出的篮球会下落 | D. | 坐公交车有位子 |
 如图,一艘客轮在大平洋中航行,所在位置是A(140°,20°),10小时后到达B地,用坐标表示B地的位置是(120°,30°).
如图,一艘客轮在大平洋中航行,所在位置是A(140°,20°),10小时后到达B地,用坐标表示B地的位置是(120°,30°).