题目内容
8.某厂家计划生产甲、乙两种产品共20件,两种产品的生产成本是生产数量的一次函数,如表提供了部分生产数据,设甲产品的生产数量为x件,| 生产数量(件) | 1 | 2 | … |
| 甲产品单价(元/件) | 27 | 24 | … |
| 乙产品单价(元/件) | 58 | 56 | … |
(2)若生产甲产品的数量不少于乙产品数量的$\frac{2}{3}$,乙产品的生产成本不高于40元,求该厂家有几种生产方案?
(3)若该厂家分别以80元/件和70元/件的出厂价销售甲、乙两种产品,且全部销售完,总利润可能达到1100元吗?如果能,请求出生产方案;如果不能,请说明理由.
分析 (1)根据给定数据利用待定系数法即可求出y1与x的关系式;
(2)设乙产品的生产成本为y2(元/件),乙产品的生产数量为(20-x)件,根据给定数据利用待定系数法即可求出y2与x的关系式,再根据生产甲产品的数量不少于乙产品数量的$\frac{2}{3}$以及乙产品的生产成本不高于40元,即可得出关于x一元一次不等式组,解之即可得出x的取值范围,由此即可找出厂家的生产方案;
(3)设总利润为w,根据总利润=甲产品单件利润×生产数量+乙产品单件利润×生产数量即可得出w关于x的关系式,令w≥1100即可得出关于x的一元二次不等式,解之即可得出x的取值范围,结合(2)的结论即可找出厂家的生产方案.
解答 解:(1)设y1与x的关系式为y1=kx+b(k≠0),
将(1,27)、(2,24)代入y1=kx+b中,
$\left\{\begin{array}{l}{k+b=27}\\{2k+b=24}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=-3}\\{b=30}\end{array}\right.$,
∴y1与x的关系式为y1=-3x+30.
(2)设乙产品的生产成本为y2(元/件),乙产品的生产数量为(20-x)件,
利用待定系数法即可得出y2=-2(20-x)+60=2x+20.
∵生产甲产品的数量不少于乙产品数量的$\frac{2}{3}$,乙产品的生产成本不高于40元,
∴$\left\{\begin{array}{l}{2x+20≤40}\\{x≥\frac{2}{3}(20-x)}\end{array}\right.$,
解得:8≤x≤10.
∴该厂有三种生产方案.方案一:生产8件甲产品,生产12件乙产品;方案二:生产9件甲产品,生产11件乙产品;方案三:生产10件甲产品,生产10件乙产品.
(3)设总利润为w,根据题意得:w=[80-(-3x+30)]x+[70-(2x+20)](20-x)=5x2-40x+1000,
令w=5x2-40x+1000≥1100,
解得:x≤-2或x≥10.
结合(2)可知x=10.
∴当生产10件甲产品,生产10件乙产品时,总利润为1100元.
点评 本题考查了一次函数的应用、待定系数法求一次函数解析式、一元一次不等式组的应用以及解一元二次不等式,解题的关键是:(1)根据给定数据利用待定系数法求出函数关系式;(2)根据数量关系找出关于x的一元一次不等式组;(3)根据数量关系找出关于x的一元二次不等式.本题属于中档题,难度不大,解决该体系题目时,找准数量关系是解题的突破点.

| A. | x-y2=1 | B. | $\sqrt{{x}^{2}-1}$=0 | C. | $\frac{1}{{x}^{2}}$-1=0 | D. | $\frac{{x}^{2}}{2}$+$\frac{x}{3}$-1=0 |
| A. | 2392元 | B. | 2394元 | C. | 2388元 | D. | 2412元 |
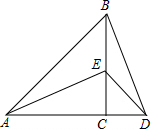 如图,已知△ABC与△CDE都是等腰直角三角形,连结AE与BD,试探究线段AE与BD的数量关系和位置关系.
如图,已知△ABC与△CDE都是等腰直角三角形,连结AE与BD,试探究线段AE与BD的数量关系和位置关系. 如图,△ABC三个顶点的坐标分别为A(-1,1),B(-4,2),C(-3,4).
如图,△ABC三个顶点的坐标分别为A(-1,1),B(-4,2),C(-3,4). 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.
如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.