题目内容
13. 如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.
如图,已知在矩形ABCD中,AB=a,BC=b,点E是线段AD边上的任意一点(不含端点A、D),连接BE、CE.(1)若a=5,sin∠ACB=$\frac{5}{13}$,解答下列问题:
①填空:b=12;
②当BE⊥AC时,求出此时AE的长;
(2)设AE=x,试探索点E在线段AD上运动过程中,使得△ABE与△BCE相似时,请写x、a、b三者的关系式.
分析 (1)①在矩形ABCD中,得到∠ABC=90°,解直角三角形即可得到结果;
②只要证明△AEB∽△BAC,得 $\frac{AE}{AB}$=$\frac{AB}{BC}$,由此即可解决问题.
(2)分两种情形讨论①当△ABE∽△EBC时,②当△BAE∽△CEB时,分别求解即可.
解答 解:(1)①∵在矩形ABCD中,
∴∠ABC=90°,
∵AB=a=5,sin∠ACB=$\frac{5}{13}$,
∴$\frac{AB}{AC}$=$\frac{5}{13}$,
∴AC=13,
∴BC=$\sqrt{A{C}^{2}-A{B}^{2}}$=12,
∴b=12;
故答案为:12;
②∵BE⊥AC,
∴∠EBC+∠ACB=90°
又∵∠ABE+∠EBC=90°,
∴∠ABE=∠ACB,
又∵∠BAE=∠ABC=90°,
∴△AEB∽△BAC,
∴$\frac{AE}{AB}$=$\frac{AB}{BC}$,
即 $\frac{AE}{5}$=$\frac{5}{12}$,
∴AE=$\frac{25}{12}$;
(2)∵点E在线段AD上的任一点,且不与A、D重合,
∴当△ABE与△BCE相似时,则∠BEC=90°,
①当△ABE∽△EBC时,∠ABE=∠EBC=45°,
∴△EBC是等腰直角三角形,
BC=$\sqrt{2}$BE,BE=$\sqrt{2}$AB,
∴BC=2AB,即b=2a,x=a或x=$\frac{1}{2}$b.
②当△BAE∽△CEB
∴∠ABE=∠BCE,
又∵BC∥AD,
∴∠DEC=∠BCE,
∴∠ABE=∠DEC,
又∵∠BAE=∠EDC=90°,
∴△BAE∽△EDC,
∴$\frac{AE}{DC}$=$\frac{AB}{DE}$,
即 $\frac{x}{a}$=$\frac{a}{b-x}$,
∴x2-bx+a2=0,
即(x-$\frac{b}{2}$)2=$\sqrt{\frac{{b}^{2}-4{a}^{2}}{4}}$,
当b2-4a2≥0,
∵a>0,b>0,
∴b≥2a,
即b≥2a时,x=$\frac{b±\sqrt{{b}^{2}-4{a}^{2}}}{2}$.
综上所述:当a、b满足条件b=2a时△BAE∽△CEB,此时x=$\frac{1}{2}$b(或x=a);当a、b满足条件b>2a时△BAE∽△CEB,此时x=$\frac{b±\sqrt{{b}^{2}-4{a}^{2}}}{2}$.
点评 本题考查了相似三角形的判定和性质,矩形的性质,一元二次方程根的情况,锐角三角函数等知识,解题的关键是学会用分类讨论思想思考问题,属于中考压轴题.

 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CD交AO于点E,DE=4,CE=5,则tan∠B的值为( )
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CD交AO于点E,DE=4,CE=5,则tan∠B的值为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
(1)请你在下表的空格里填写一个适当的式子:
| 第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
| a | a+2 | a+4 | … |
(3)求当a=20时,第10排的座位数是多少?
| A. | (a+3b)(a-3b)=a2-3b2 | B. | (-a+3b)(a-3b)=-a2-9b2 | ||
| C. | (a-3b)(a-3b)=a2-9b2 | D. | (-a-3b)(-a+3b)=a2-9b2 |
| 生产数量(件) | 1 | 2 | … |
| 甲产品单价(元/件) | 27 | 24 | … |
| 乙产品单价(元/件) | 58 | 56 | … |
(2)若生产甲产品的数量不少于乙产品数量的$\frac{2}{3}$,乙产品的生产成本不高于40元,求该厂家有几种生产方案?
(3)若该厂家分别以80元/件和70元/件的出厂价销售甲、乙两种产品,且全部销售完,总利润可能达到1100元吗?如果能,请求出生产方案;如果不能,请说明理由.
| A. | 缩小10倍 | B. | 扩大10倍 | C. | 扩大100倍 | D. | 不改变 |
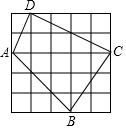 如图,小方格都是边长为1的正方形.求四边形ABCD的面积和周长.
如图,小方格都是边长为1的正方形.求四边形ABCD的面积和周长.