题目内容
17．点A（a，4）与点B（-3，b）关于y轴对称，则a=□，b=□．（ ）| A． | 4 3 | B． | 3 4 | C． | 5 6 | D． | 6 5 |
分析 利用关于y轴对称点的性质，横坐标互为相反数，纵坐标不变．即点P（x，y）关于y轴的对称点P′的坐标是（-x，y），进而得出答案．
解答 解：∵点A（a，4）与点B（-3，b）关于y轴对称，
∴a=3，b=4，
故选：B．
点评 此题主要考查了关于y轴对称点的性质，正确把握横纵坐标的性质是解题关键．
练习册系列答案
相关题目
7．
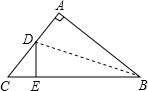如图，在Rt△ABC中，∠A=90°，AC=6cm，AB=8cm，把AB边翻折，使AB边落在BC边上，点A落在点E处，折痕为BD，则tan∠DBE的值为（ ）
如图，在Rt△ABC中，∠A=90°，AC=6cm，AB=8cm，把AB边翻折，使AB边落在BC边上，点A落在点E处，折痕为BD，则tan∠DBE的值为（ ）| A． | $\frac{1}{3}$ | B． | $\frac{3}{10}$ | C． | $\frac{3\sqrt{73}}{73}$ | D． | $\frac{\sqrt{10}}{10}$ |
8．如果x是最大的负整数，y是绝对值最小的整数，则-x2015+y的值是（ ）
| A． | 2015 | B． | -1 | C． | 1 | D． | -2015 |
5．已知点A（m-1，3）与点B（2，n-1）关于x轴对称，则（m+n）2015的值为（ ）
| A． | 0 | B． | -1 | C． | 1 | D． | 32015 |
2．如果|a+1|+（b-2）2=0，则（a+b）2015+a2的值为（ ）
| A． | 0 | B． | 2 | C． | -2 | D． | 1 |
6．
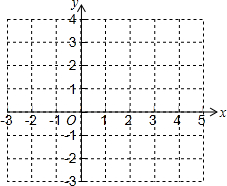对于抛物线y=x2-4x+3．
（1）它与x轴交点的坐标为（1，0），（3，0），与y轴交点的坐标为（0，3）；
（2）在坐标系中利用描点法画出此抛物线：
（3）根据图象说明：当x为何值时，函数y随着x的增大而增大？当x为何值时，函数y随着x的增大而减小？
对于抛物线y=x2-4x+3．（1）它与x轴交点的坐标为（1，0），（3，0），与y轴交点的坐标为（0，3）；
（2）在坐标系中利用描点法画出此抛物线：
| x | … | … | |||||
| y | … | … |