题目内容
13.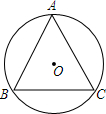 如图,⊙O的半径为10,则⊙O的内接正三角形ABC的边长为10$\sqrt{3}$.
如图,⊙O的半径为10,则⊙O的内接正三角形ABC的边长为10$\sqrt{3}$.
分析 连接OA,OB,过O作OD⊥AB于D,由垂径定理得到AD=BD,由含30°直角三角形的性质求出OD,得出AD,即可得出结果.
解答 解:连接OA,OB,过O作OD⊥AB于D,如图所示: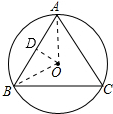
∴AD=BD,
∵△ABC为等边三角形,
∴∠C=60°,
∴∠AOB=120°,
又∵OA=OB,
∴∠OAB=∠OBA=30°,
∴OD=$\frac{1}{2}$OA=5,
∴AD=$\sqrt{3}$OD=5$\sqrt{3}$,
∴AB=2AD=10$\sqrt{3}$.
故答案为:10$\sqrt{3}$.
点评 此题考查了垂径定理,勾股定理,等边三角形的性质,以及含30°直角三角形的性质;熟练掌握等边三角形的性质,求出AD是解决问题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
4.已知2x2+3x+1的值是10,则代数式4x2+6x+1的值是( )
| A. | 10 | B. | 0 | C. | 19 | D. | 20 |
 如图,化简|a+b|-|a|+|b|=2a+2b.
如图,化简|a+b|-|a|+|b|=2a+2b.
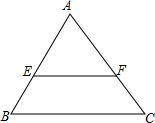 如图,△ABC中,EF∥BC,且EF=$\frac{2}{3}$BC=4cm,△AEF的周长为10cm,求BCFE的周长.
如图,△ABC中,EF∥BC,且EF=$\frac{2}{3}$BC=4cm,△AEF的周长为10cm,求BCFE的周长.