题目内容
已知△ABC的BC边上的中线是△ABC的一条角平分线.求证:△ABC是等腰三角形.
考点:等腰三角形的判定
专题:证明题
分析:设BC边上的中线为AD,作DE⊥AB于E,DF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得DE=DF,再利用“HL”证明Rt△BDE和Rt△CDF全等,然后根据全等三角形对应边相等即可证明.
解答: 证明:如图,设BC边上的中线为AD,作DE⊥AB于E,DF⊥AC于F,
证明:如图,设BC边上的中线为AD,作DE⊥AB于E,DF⊥AC于F,
∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵AD是BC边的中线,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
,
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C.
∴AB=AC,
∴△ABC是等腰三角形.
 证明:如图,设BC边上的中线为AD,作DE⊥AB于E,DF⊥AC于F,
证明:如图,设BC边上的中线为AD,作DE⊥AB于E,DF⊥AC于F,∵AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,
∴DE=DF,
∵AD是BC边的中线,
∴BD=CD,
在Rt△BDE和Rt△CDF中,
|
∴Rt△BDE≌Rt△CDF(HL),
∴∠B=∠C.
∴AB=AC,
∴△ABC是等腰三角形.
点评:本题考查了等腰三角形的判定,角的平分线的性质,直角三角形的全等判定与性质,要证边相等,想办法证明边所在的三角形全等,是常用的方法之一,要熟练掌握并灵活运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿以2cm/s的速度向点D移动.经过多长时间P、Q两点的距离是10?
如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿以2cm/s的速度向点D移动.经过多长时间P、Q两点的距离是10?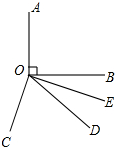 如图所示,OA⊥OB,OC⊥OE,OD为∠BOC的平分线,∠BOE=16°,求∠DOE的度数.
如图所示,OA⊥OB,OC⊥OE,OD为∠BOC的平分线,∠BOE=16°,求∠DOE的度数. 如图,正六边形ABCDEF中.阴影部分面积为12
如图,正六边形ABCDEF中.阴影部分面积为12