题目内容
8．①代数式$\sqrt{x-1}$在实数范围里有意义，则x的取值范围是x≥1；②化简$\sqrt{12{a}^{3}}$的结果是2a$\sqrt{3a}$；
③在实数范围里因式分解x2-3=（x+$\sqrt{3}$）（x-$\sqrt{3}$）．
分析 ①根据被开方数大于等于0列式计算即可得解；
②根据二次根式的性质化简即可；
③利用平方差公式分解因式即可．
解答 解：①由x-1≥解得，x≥1；
②$\sqrt{12{a}^{3}}$=2a$\sqrt{3a}$；
③x2-3=（x+$\sqrt{3}$）（x-$\sqrt{3}$）．
故答案为：x≥1；2a$\sqrt{3a}$；（x+$\sqrt{3}$）（x-$\sqrt{3}$）．
点评 本题考查了二次根式有意义的条件，利用二次根式的性质化简以及实数范围内的因式分解，二次根式的被开方数是非负数．
练习册系列答案
相关题目
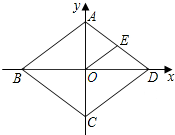如图，在菱形ABCD中，对角线AC，BD相交于点O，AC=12，BD=16，E为AD中点，点P在x轴上移动．若△POE为等腰三角形，请写出所有符合要求的点P的坐标（5，0）（-5，0）（8，0）（$\frac{25}{8}$，0）．
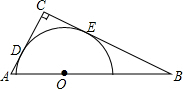如图，Rt△ABC中，∠ACB=90°，AC=4，BC=6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则AD的长为（ ）
20．已知a，b为实数，则点P（$\sqrt{1+{a}^{2}}$-1，-|b-1|-1）落在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
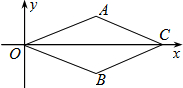如图，在平面直角坐标系中，菱形OABC的顶点O、A的坐标分别是（0，0），（2，1），则顶点C的坐标是（4，0）．