题目内容
8.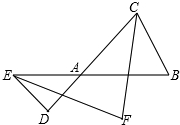 如图,E和D分别在△ABC的边BA和CA的延长线上,CF,EF分别平分∠ACB和∠AED,若∠B=60°,∠D=40°,则∠F的大小是50.
如图,E和D分别在△ABC的边BA和CA的延长线上,CF,EF分别平分∠ACB和∠AED,若∠B=60°,∠D=40°,则∠F的大小是50.
分析 由CF、EF分别平分∠ACB和∠AED,得∠3=∠4,∠1=∠2,所以有∠3+∠B=∠2+∠F;∠3+∠4+∠B=∠1+∠2+∠D,即2∠3+∠B=2∠2+∠D,而∠B=70°,∠D=40°,于是由两个等式即可求出∠F.
解答  解:如图,
解:如图,
∵CF、EF分别平分∠ACB和∠AED,
∴∠3=∠4,∠1=∠2,
而∠3+∠B=∠2+∠F;
∠3+∠4+∠B=∠1+∠2+∠D,即2∠3+∠B=2∠2+∠D,
又∵∠B=60°,∠D=40°,
∴∠3+60°=∠2+∠F①,
2∠3+60°=2∠2+40°②,
①×2-②得,60°=2∠F-40°,
解得∠F=50°.
故答案为:50°.
点评 本题考查了三角形的内角和定理,角平分线的性质,熟练掌握三角形的内角和是解题的关键.

练习册系列答案
相关题目
20.在△ABC中,∠A-∠C=∠B,那么△ABC是( )
| A. | 等边三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 直角三角形 |
17.在下面的图形中是正方体的展开图的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,菱形ABCD中,∠B=60°,∠DAF=40°,∠EAF=60°
如图,菱形ABCD中,∠B=60°,∠DAF=40°,∠EAF=60° 画出如图所示物体的正投影(正三棱柱).
画出如图所示物体的正投影(正三棱柱).
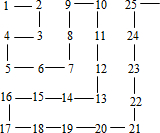 将正整数从1开始,按如图所表示的规律排列.规定图中第m行、第n列的位置记作(m,n),如正整数8的位置是(2,3),则正整数137的位置记作(12,8).
将正整数从1开始,按如图所表示的规律排列.规定图中第m行、第n列的位置记作(m,n),如正整数8的位置是(2,3),则正整数137的位置记作(12,8).