题目内容
20．在△ABC中，∠A-∠C=∠B，那么△ABC是（ ）| A． | 等边三角形 | B． | 锐角三角形 | C． | 钝角三角形 | D． | 直角三角形 |
分析 根据三角形内角和定理得到∠A+∠B+∠C=180°，则∠A+∠B=180°-∠C，由∠A=∠B-∠C变形得∠A+∠B=∠C，则180°-∠C=∠C，解得∠C=90°，即可判断△ABC的形状．
解答 解：∵∠A+∠B+∠C=180°，
∴∠C+∠B=180°-∠A，
而∠A-∠C=∠B，
∴∠C+∠B=∠A，
∴180°-∠A=∠A，解得∠A=90°，
∴△ABC为直角三角形．
故选D．
点评 本题考查了三角形内角和定理：三角形的内角和为180°，直角三角形的判定，熟记掌握三角形的内角和是解题的关键．
练习册系列答案
相关题目
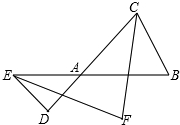如图，E和D分别在△ABC的边BA和CA的延长线上，CF，EF分别平分∠ACB和∠AED，若∠B=60°，∠D=40°，则∠F的大小是50．
某公司的外墙壁贴的是反光玻璃，晚上两根木棒的影子如图（短木棒的影子是玻璃反光形成的），请确定图中路灯灯泡所在的位置．