题目内容
如图,已知sin∠ABC=| 1 |
| 3 |
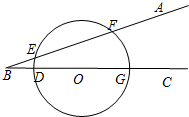 两点,EF=2
两点,EF=2| 3 |
(1)求BO的长;
(2)点P在射线BC上,以点P为圆心作圆,使得⊙P同时与⊙O和射线BA相切,求所有满足条件的⊙P的半径.
分析:(1)连接EO,过点O作OH⊥BA于点H.利用垂径定理构造直角三角形求得OH,然后利用告诉的∠B的正弦值求得OB;
(2)⊙P同时与⊙O和射线BA相切应分两种情况分类讨论:①当⊙P与⊙O外切;②当⊙P与⊙O内切.
(2)⊙P同时与⊙O和射线BA相切应分两种情况分类讨论:①当⊙P与⊙O外切;②当⊙P与⊙O内切.
解答: 解:(1)连接EO,过点O作OH⊥BA于点H.
解:(1)连接EO,过点O作OH⊥BA于点H.
∵EF=2
,∴EH=
.
∵⊙O的半径为2,即EO=2,
∴OH=1.在Rt△BOH中,
∵sin∠ABC=
,
∴BO=3.
(2)当⊙P与直线相切时,过点P的半径垂直此直线.
(a)当⊙P与⊙O外切时,
①⊙P与⊙O切于点D时,⊙P与射线BA相切,
sin∠ABC=
=
,得到:rP=
;
②⊙P与⊙O切于点G时,⊙P与射线BA相切,
sin∠ABC=
=
,得到:rP=
.
(b)当⊙P与⊙O内切时,
①⊙P与⊙O切于点D时,⊙P与射线BA相切,
sin∠ABC=
=
,得到:rP=
;
②⊙P与⊙O切于点G时,⊙P与射线BA相切,
sin∠ABC=
=
,得到:rP=
.
综上所述:满足条件的⊙P的半径为
、
、
、
 解:(1)连接EO,过点O作OH⊥BA于点H.
解:(1)连接EO,过点O作OH⊥BA于点H.∵EF=2
| 3 |
| 3 |
∵⊙O的半径为2,即EO=2,
∴OH=1.在Rt△BOH中,
∵sin∠ABC=
| 1 |
| 3 |
∴BO=3.
(2)当⊙P与直线相切时,过点P的半径垂直此直线.
(a)当⊙P与⊙O外切时,
①⊙P与⊙O切于点D时,⊙P与射线BA相切,
sin∠ABC=
| rP |
| 1-rP |
| 1 |
| 3 |
| 1 |
| 4 |
②⊙P与⊙O切于点G时,⊙P与射线BA相切,
sin∠ABC=
| rp |
| 5+rp |
| 1 |
| 3 |
| 5 |
| 2 |
(b)当⊙P与⊙O内切时,
①⊙P与⊙O切于点D时,⊙P与射线BA相切,
sin∠ABC=
| rP |
| 1+rP |
| 1 |
| 3 |
| 1 |
| 2 |
②⊙P与⊙O切于点G时,⊙P与射线BA相切,
sin∠ABC=
| rP |
| 5-rP |
| 1 |
| 3 |
| 5 |
| 4 |
综上所述:满足条件的⊙P的半径为
| 1 |
| 4 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
点评:本题综合考查了直线与圆相切和两圆相切的知识,对学生建立系统的与圆相切有关的知识体系有很好的促进作用.

练习册系列答案
相关题目
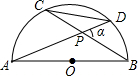 如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么CD:AB等于( )
如图,已知AB是半圆O的直径,弦AD、BC相交于点P,若∠DPB=α,那么CD:AB等于( )| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
 如图,已知△ABC的外接圆⊙O的半径为1,D、E分别是AB、AC上的点,BD=2AD,EC=2AE,则sin∠BAC的值等于线段( )
如图,已知△ABC的外接圆⊙O的半径为1,D、E分别是AB、AC上的点,BD=2AD,EC=2AE,则sin∠BAC的值等于线段( )| A、DE的长 | ||
| B、BC的长 | ||
C、
| ||
D、
|
 ,⊙O的半径为2,圆心O在射线BC上,⊙O与射线BA相交于E、F
,⊙O的半径为2,圆心O在射线BC上,⊙O与射线BA相交于E、F 两点,EF=
两点,EF= .
. ,⊙O的半径为2,圆心O在射线BC上,⊙O与射线BA相交于E、F两点,EF=
,⊙O的半径为2,圆心O在射线BC上,⊙O与射线BA相交于E、F两点,EF= .
.