题目内容
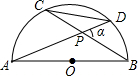如图，已知AB是半圆O的直径，弦AD、BC相交于点P，若∠DPB=α，那么CD：AB等于（ ）| A、sinα | ||
| B、cosα | ||
| C、tanα | ||
D、
|
分析：连接BD得到∠ADB是直角，再利用两三角形相似对应边成比例即可求解．
解答：
解：连接BD，由AB是直径得，∠ADB=90°．
∵∠C=∠A，∠CPD=∠APB，
∴△CPD∽△APB，
∴CD：AB=PD：PB=cosα．
故选B．
解：连接BD，由AB是直径得，∠ADB=90°．∵∠C=∠A，∠CPD=∠APB，
∴△CPD∽△APB，
∴CD：AB=PD：PB=cosα．
故选B．
点评：本题利用了圆周角定理和相似三角形的判定和性质及锐角三角函数的概念求解．
练习册系列答案
阅读快车系列答案
相关题目
如图，已知AB是半圆O的直径，∠BAC=32°，D是 |
| AC |
| A、25° | B、29° |
| C、30° | D、32° |
如图，已知AB是半圆的直径，∠BAC=20°，D是
（2012•葫芦岛一模）如图，已知AB是半圆O的直径，AB=10，点P是半圆周上一点，连接AP、BP，并延长BP至点C，使CP=BP，过点C作CE⊥AB，点E为垂足，CE交AP于点F，连接OF．