题目内容
设关于x的方程2x2+ax+2=0的两根为α,β,且α2+β2=
+
,则α=
| 1 |
| α |
| 1 |
| β |
-4
-4
.分析:先根据根与系数的关系得到α+β=-
,αβ=1,再变形α2+β2=
+
得(α+β)2-2αβ=
,则
-2=-
,解方程得a1=-4,a2=-2,然后根据根的判别式确定a的值.
| a |
| 2 |
| 1 |
| α |
| 1 |
| β |
| α+β |
| αβ |
| a2 |
| 4 |
| a |
| 2 |
解答:解:根据题意得α+β=-
,αβ=1,
∵α2+β2=
+
,
∴(α+β)2-2αβ=
,
∴
-2=-
,
解得a1=-4,a2=2,
∵△=a2-4×2×2≥0,
∴a=-4.
故答案为-4.
| a |
| 2 |
∵α2+β2=
| 1 |
| α |
| 1 |
| β |
∴(α+β)2-2αβ=
| α+β |
| αβ |
∴
| a2 |
| 4 |
| a |
| 2 |
解得a1=-4,a2=2,
∵△=a2-4×2×2≥0,
∴a=-4.
故答案为-4.
点评:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程两个为x1,x2,则x1+x2=-
,x1•x2=
.
| b |
| a |
| c |
| a |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)
(在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)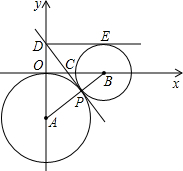 上,过P点作两圆的公切线DP交y轴于D,交x轴于C,
上,过P点作两圆的公切线DP交y轴于D,交x轴于C, +
+ ,则α=________.
,则α=________.