题目内容
8.计算:(1)化简:$\frac{5x+3y}{{x}^{2}-{y}^{2}}-\frac{2x}{{x}^{2}-{y}^{2}}$
(2)解方程:$\frac{3-x}{x-4}+\frac{1}{4-x}=1$.
分析 (1)先进行同分母的减法运算,然后把分母因式分解后约分即可;
(2)先去分母把分式方程化为整式方程,解整式方程得到x=3,然后进行检验确定原方程的解.
解答 解:(1)原式=$\frac{5x+3y-2x}{(x+y)(x-y)}$
=$\frac{3(x+y)}{(x+y)(x-y)}$
=$\frac{3}{x-y}$;
(2)去分母得3-x-1=x-4,
解得x=3,
经验:当x=3时,x-4≠0,
所以原方程的解为x=3.
点评 本题考查了分式的加减法:同分母分式加减法法则:同分母的分式相加减,分母不变,把分子相加减.也考查了解分式方程.

练习册系列答案
相关题目
19.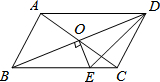 如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )
如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )
 如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )
如图,?ABCD的对角线相交于点O,且AB≠AD,过点O作OE⊥BD交BC于点E.若△CDE的周长为8cm,则?ABCD的周长为( )| A. | 8cm | B. | 12cm | C. | 16cm | D. | 24cm |
16.班主任老师在七年级(1)班新生分组时发现,若每组7人则多2人,若每组8人则少4人,那么这个班的学生人数是( )人.
| A. | 40 | B. | 44 | C. | 51 | D. | 56 |
3.厦深铁路起点厦门北站,终点深圳北站.汕尾鲘门站、深圳坪山站在其沿线上,它们之间有惠东站、惠州南站,那么在鲘门站和坪山站之间需准备火车票的种数为(任何两站之间,往返两种车票)( )
| A. | 8种 | B. | 10种 | C. | 12种 | D. | 14种 |
13.一个两位数,各数位上的数字之和为8,个位数字与十位数字互换位置后所得的两位数比原两位数小18,则原两位数( )
| A. | 26 | B. | 62 | C. | 53 | D. | 35 |
18.解方程组$\left\{\begin{array}{l}{2m-4n=6①}\\{4m-5n=18②}\end{array}\right.$的最佳方案是( )
| A. | 由①得m=3+2n,再代入② | B. | 由②得m=$\frac{9}{2}$+$\frac{5}{4}$n,再代入① | ||
| C. | 由①得n=$\frac{1}{2}m$-$\frac{3}{2}$,再代入② | D. | 由①得2m=6+4n,再代入② |
 如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A、C分别在坐标轴上,顶点B的坐标为(6,4),E为AB的中点,过点D(8,0)和点E的直线分别与BC、y轴交于点F、G.