题目内容
在△ABC中,BC=24cm,外心O到BC的距离为5cm,求△ABC的外接圆半径.
考点:三角形的外接圆与外心
专题:
分析:根据外心的性质可知OD垂直平分BC,可知△BOD为直角三角形,BD=
BC=12,OD=5,由勾股定理可求半径OB.
| 1 |
| 2 |
解答::解:∵O为外心,OD⊥BC,
∴BD=
BC=12,又OD=5,
∴由勾股定理,得
OB=
=
=13,
∴△ABC的外接圆的半径是13cm.
∴BD=

| 1 |
| 2 |
∴由勾股定理,得
OB=
| BD2+AD2 |
| 122+52 |
∴△ABC的外接圆的半径是13cm.
点评:本题考查了三角形的外心的性质和勾股定理等知识的综合应用,得出BD的长是解题关键.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
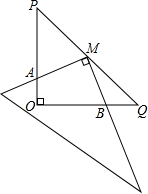 如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB.
如图,在Rt△POQ中,OP=OQ,M是PQ的中点,把一三角尺的直角顶点放在M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB. 实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
实践操作:如图,△ABC是直角三角形,∠ABC=90°,利用直尺和圆规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).