题目内容
12.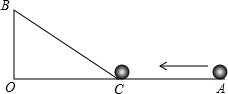 如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=9cm,OB=3cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿BC方向匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
分析 根据小球滚动的速度与机器人行走的速度相等,运动时间相等得出BC=CA.设AC为x,则OC=9-x,根据勾股定理即可得出结论.
解答 解:∵小球滚动的速度与机器人行走的速度相等,运动时间相等,
∴BC=CA.
设AC为x,则OC=9-x,
由勾股定理得:OB2+OC2=BC2,
又∵OA=9,OB=3,
∴32+(9-x)2=x2,
解方程得出x=5.
∴机器人行走的路程BC是5cm.
点评 本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
2.若三角形三个内角度数的比为1:2:3,则这个三角形的最小角是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
 如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长.
如图,△ABC沿边BA平移到△DEF的位置,它们重叠部分(即图中阴影部分)的面积是△ABC面积的$\frac{1}{9}$,若AB=2,求△ABC移动的距离BE的长. 如图,⊙O是等边三角形ABC的外接圆,OD⊥AB,OE⊥AC,D、E为垂足,则OD=OE(填“>”“=”“<”)
如图,⊙O是等边三角形ABC的外接圆,OD⊥AB,OE⊥AC,D、E为垂足,则OD=OE(填“>”“=”“<”)