题目内容
13.若y=$\sqrt{1-x}$+$\sqrt{x-\frac{1}{2}}$的最大值为a,最小值为b,则a2+b2的值为( )| A. | 1 | B. | 1.5 | C. | 2 | D. | 2.5 |
分析 首先根据二次根式有意义得1-x≥0,且x-$\frac{1}{2}$≥0,从而得到$\frac{1}{2}$≤x≤1.然后等式两边分别平方后得到y2=$\frac{1}{2}$+2$\sqrt{-{x}^{2}+\frac{3}{2}x-\frac{1}{2}}$=$\frac{1}{2}$+2$\sqrt{-(x-\frac{3}{4})^{2}+\frac{1}{16}}$,得到当x=$\frac{3}{4}$时,y2取到最大值1,故a=1.当x=$\frac{1}{2}$或1时,y2取到最小值$\frac{1}{2}$,故b=$\frac{\sqrt{2}}{2}$,从而求得代数式的值.
解答 解:由1-x≥0,且x-$\frac{1}{2}$≥0,得$\frac{1}{2}$≤x≤1.
y2=$\frac{1}{2}$+2$\sqrt{-{x}^{2}+\frac{3}{2}x-\frac{1}{2}}$=$\frac{1}{2}$+2$\sqrt{-(x-\frac{3}{4})^{2}+\frac{1}{16}}$.
由于$\frac{1}{2}$<$\frac{3}{4}$<1,
所以当x=$\frac{3}{4}$时,y2取到最大值1,故a=1.
当x=$\frac{1}{2}$或1时,y2取到最小值$\frac{1}{2}$,故b=$\frac{\sqrt{2}}{2}$.
所以:a2+b2=$\frac{3}{2}$=1.5.
故选B.
点评 本题考查了无理函数的最值,特别是确定自变量的取值范围是解答本题的关键,将题目中的等式两边平方是解决无理函数的一种重要方法,难度偏大.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18.盐城市中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.(方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].
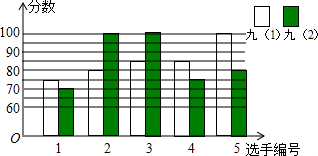
(1)根据图示填写下表;
| 班级 | 平均数(分) | 中位数(分) | 众数(分) |
| 九(1) | 85 | 85 | 85 |
| 九(2) | 85 | 80 | 100 |
(3)计算两班复赛成绩的方差.(方差公式:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

3.下列说法中错误的是( )
| A. | 成轴对称的两个图形的对应点连线的垂直平分线是它们的对称轴 | |
| B. | 关于某条直线对称的两个图形全等 | |
| C. | 若两个图形沿某条直线对折后能够完全重合,我们称两个图形成轴对称 | |
| D. | 全等的三角形一定关于某条直线对称 |
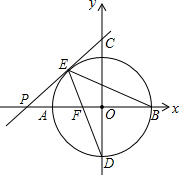 ⊙O交坐标轴于A、B、C、D四点,P为x轴上一点,PE切⊙O于E,连接ED、EB,PA=4,PE=8
⊙O交坐标轴于A、B、C、D四点,P为x轴上一点,PE切⊙O于E,连接ED、EB,PA=4,PE=8 一平面镜以与水平面成45°角固定在水平面上,如图所示,一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像将竖直向下.
一平面镜以与水平面成45°角固定在水平面上,如图所示,一小球以1米/秒的速度沿桌面向平面镜匀速滚去,则小球在平面镜里所成的像将竖直向下.