题目内容
 如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,点A落在平面内的A′处,∠B=50°,则∠BDA′的度数是
如图,已知△ABC中,DE∥BC,将△ADE沿DE翻折,点A落在平面内的A′处,∠B=50°,则∠BDA′的度数是考点:翻折变换(折叠问题)
专题:
分析:由两直线平行,同位角相等推知∠ADE=∠B=50°;由折叠的性质知∠ADE=∠A′DE,所以∠BDA′=180°-2∠B=80°.
解答:解:∵DE∥BC,
∴∠ADE=∠B=50°(两直线平行,同位角相等);
又∵∠ADE=∠A′DE,
∴∠A′DA=2∠B,
∴∠BDA′=180°-2∠B=80°
故答案为:80°.
∴∠ADE=∠B=50°(两直线平行,同位角相等);
又∵∠ADE=∠A′DE,
∴∠A′DA=2∠B,
∴∠BDA′=180°-2∠B=80°
故答案为:80°.
点评:本题考查了平行线的性质、翻折变换(折叠问题).折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
方程x2-6x+9=0的根的情况是( )
| A、没有实数根 |
| B、有且仅有一个实数根 |
| C、有两个相等的实数根 |
| D、有两个不相等的实数根 |
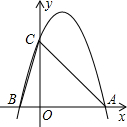 如图,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
如图,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C. 如图,在?ABCD中,E为BC的中点,连接DE并延长DE交AB的延长线于点F.
如图,在?ABCD中,E为BC的中点,连接DE并延长DE交AB的延长线于点F. 如图,在△ABC中,AB=AC,BC=12,tanC=
如图,在△ABC中,AB=AC,BC=12,tanC=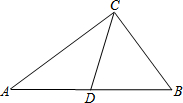 如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在CB的延长线A′处,点D落在点D′处,则D′B长为
如图,在Rt△ABC中,∠ACB=90°,AC=4,BC=3,点D为AB的中点,将△ACD绕着点C逆时针旋转,使点A落在CB的延长线A′处,点D落在点D′处,则D′B长为