题目内容
8.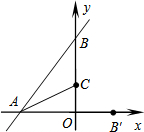 直线y=$\frac{4}{3}$x+4与x轴,y轴分别交于点A和点B,C是OB上一点.若将△ABO沿AC折叠,点B恰好落在x轴上的点B′处,则点C的坐标是C(0,$\frac{3}{2}$).
直线y=$\frac{4}{3}$x+4与x轴,y轴分别交于点A和点B,C是OB上一点.若将△ABO沿AC折叠,点B恰好落在x轴上的点B′处,则点C的坐标是C(0,$\frac{3}{2}$).
分析 先求出点A、B的坐标,可知OA、OB、AB的长度,再在Rt△OB′C中运用勾股定理列方程求出OC即可.
解答 解:由题意得:A(-3,0),B(0,4);
∴OA=3,OB=4.那么可得AB=5.
根据折叠的性质,易得△ABC≌△AB′C,
∴AB′=AB=5,
∴OB′=AB′-OA=2.
设OC为x.那么BC=CB′=4-x.那么x2+22=(4-x)2,
解得x=$\frac{3}{2}$,
∴C(0,$\frac{3}{2}$).
故答案为:C(0,$\frac{3}{2}$).
点评 本题考查了折叠的性质、勾股定理、一次函数的综合运用,根据折叠的性质运用勾股定理列出方程是解决问题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
20.在数轴上截取从0到3的对应线段AB,实数m对应AB上的点M,如图1;将AB折成正三角形,使点A、B重合于点P,如图2;建立平面直角坐标系,平移此三角形,使它关于y轴对称,且点P的坐标为(0,2),PM的延长线与x轴交于点N(n,0),如图3,当m=$\sqrt{3}$时,n的值为( )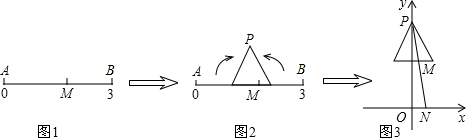

| A. | 4-2$\sqrt{3}$ | B. | 2$\sqrt{3}$-4 | C. | -$\frac{2}{3}\sqrt{3}$ | D. | $\frac{2}{3}\sqrt{3}$ |
 如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$
如图,△ABC中,AB=AC=4$\sqrt{5}$,cosC=$\frac{\sqrt{5}}{5}$


 已知AC∥BD∥EF,AB∥CD,BE∥DF,∠1=45°,∠2=95°,求∠3的度数.
已知AC∥BD∥EF,AB∥CD,BE∥DF,∠1=45°,∠2=95°,求∠3的度数.