Question

2．已知，如图，AB是⊙O的直径，点C为⊙O上一点，OF⊥BC于点F，交⊙O于点E，AE与BC交于点H，点D为OE的延长线上一点，且∠ODB=∠AEC．
（1）求证：BD是⊙O的切线；
（2）求证：CE²=EH•EA．

Answer 1

分析 （1）由圆周角定理和已知条件证出∠ODB=∠ABC，再证出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD是⊙O的切线；
（2）连接AC，由垂径定理得出$\widehat{BE}$=$\widehat{CE}$，得出∠CAE=∠ECB，再由公共角∠CEA=∠HEC，证明△CEH∽△AEC，得出对应边成比例$\frac{CE}{EH}$=$\frac{EA}{CE}$，即可得出结论．

解答 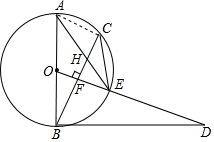（1）证明：∵∠ODB=∠AEC，∠AEC=∠ABC，
∴∠ODB=∠ABC，
∵OF⊥BC，
∴∠BFD=90°，
∴∠ODB+∠DBF=90°，
∴∠ABC+∠DBF=90°，
即∠OBD=90°，
∴BD⊥OB，
∴BD是⊙O的切线；

（2）证明：连接AC，如图所示：
∵OF⊥BC，
∴$\widehat{BE}$=$\widehat{CE}$，
∴∠CAE=∠ECB，
∵∠CEA=∠HEC，
∴△CEH∽△AEC，
∴$\frac{CE}{EH}$=$\frac{EA}{CE}$，
∴CE²=EH•EA．

点评 本题考查了切线的判定、相似三角形的判定与性质等知识，正确得出△CEH∽△AEC是解题关键．