题目内容
平面直角坐标系中，一个四边形各顶点坐标分别A（-1，-2），B（4，-2），C（4，3，D（-1，3，则四边形ABCD的形状是（ ）
| A、平行四边形 | B、长方形 |
| C、正方形 | D、无法确定 |
考点：坐标与图形性质
专题：
分析：在平面直角坐标系中，根据点的坐标画出四边形ABCD，再根据图形特点进行判断．
解答：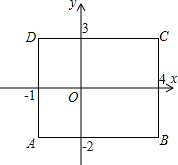
解：如图，因为A、D两点横坐标相等，B、C两点横坐标相等，
所以，AD∥y轴，BC∥y轴，
∴AD∥BC．
∵AD=BC，AD=CD，
∴四边形ABCD是菱形；
同理，CD∥AB，
∴CD⊥AD，
∴四边形ABCD是正方形．
故选：C．
解：如图，因为A、D两点横坐标相等，B、C两点横坐标相等，所以，AD∥y轴，BC∥y轴，
∴AD∥BC．
∵AD=BC，AD=CD，
∴四边形ABCD是菱形；
同理，CD∥AB，
∴CD⊥AD，
∴四边形ABCD是正方形．
故选：C．
点评：本题考查了坐标与图形性质．注意“数形结合”数学思想的应用．
练习册系列答案
相关题目
如图，等腰梯形ABCD中，AD∥BC，点E是AD延长线上的一点，且CE=CD．∠B与∠E相等吗？说明理由．方程x2-2=0的根是（ ）
A、±
| ||
B、
| ||
| C、2 | ||
| D、不能确定 |
下列式子中，是最简二次根式的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若3m=5，3n=7，则3m+n=（ ）
| A、35 |
| B、12 |
| C、57 |
| D、75 |
绝对值是本身的数是（ ）
| A、正数 | B、0 | C、非负数 | D、非正数 |
如图，在△ABC中，∠C=90°，∠A、∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于点F．下列方程是一元一次方程的是（ ）
| A、x-y=6 |
| B、x-2=x |
| C、x2+3x=1 |
| D、1+x=3 |