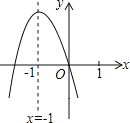题目内容
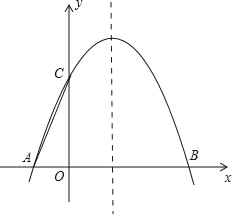
【题目】如图,直角坐标系![]() 中,一次函数
中,一次函数![]() 的图像
的图像![]() 分别与
分别与![]() 、
、![]() 轴交于
轴交于![]() 两点,正比例函数的图像
两点,正比例函数的图像![]() 与
与![]() 交于点
交于点![]() .
.

(1)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(2)求![]() 的值;
的值;
(3)在坐标轴上找一点![]() ,使以
,使以![]() 为腰的
为腰的![]() 为等腰三角形,请直接写出点
为等腰三角形,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)m=4,l2的解析式为![]() ;(2)5;(3)点P的坐标为(
;(2)5;(3)点P的坐标为(![]() ),(0,
),(0,![]() ),(0,5),(5,0),(8,0),(0,6).
),(0,5),(5,0),(8,0),(0,6).
【解析】
(1)先求得点C的坐标,再运用待定系数法即可得到l2的解析式;
(2)过C作CD⊥AO于D,CE⊥BO于E,则CD=3,CE=4,再根据A(10,0),B(0,5),可得AO=10,BO=5,进而得出S△AOC-S△BOC的值;
(3)由等腰三角形的定义,可对点P进行分类讨论,分别求出点P的坐标即可.
解:(1)把C(m,3)代入一次函数![]() ,可得
,可得
![]() ,
,
解得m=4,
∴C(4,3),
设l2的解析式为y=ax,则3=4a,
解得:a=![]() ,
,
∴l2的解析式为:![]() ;
;
(2)如图,过C作CD⊥AO于D,CE⊥BO于E,则CD=3,CE=4,

由![]() ,令x=0,则y=5;令y=0,则x=10,
,令x=0,则y=5;令y=0,则x=10,
∴A(10,0),B(0,5),
∴AO=10,BO=5,
∴S△AOC-S△BOC=![]() ×10×3
×10×3![]() ×5×4=15-10=5;
×5×4=15-10=5;
(3)∵![]() 是以
是以![]() 为腰的等腰三角形,
为腰的等腰三角形,
则点P的位置有6种情况,如图:

∵点C的坐标为:(4,3),
∴![]() ,
,
∴![]() ,
,
∴点P的坐标为:(![]() ),(0,
),(0,![]() ),(0,5),(5,0),(8,0),(0,6).
),(0,5),(5,0),(8,0),(0,6).

【题目】某“数学兴趣小组”根据学习函数的经验,对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量x的取值范围是全体实数,x与y的几组对应数值如下表:
x | … | -3 | - | -2 | -1 | 0 | 1 | 2 |
| 3 | … |
y | … | -2 | - | m | 2 | 1 | 2 | 1 | - | -2 | … |
其中m=____________;
(2)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)根据函数图象
①写出该函数的一条性质_______________;
②直线![]() 经过点(-l,2),若关于x的方程
经过点(-l,2),若关于x的方程![]() 有4个互不相等的实数根,则b的取值范围是__________________.
有4个互不相等的实数根,则b的取值范围是__________________.