题目内容
9.己知一次函数y=kx+b,当x=-3时,y=0;当x=0时,y=-4,求k与b的值,并求当x≥0时y的取值范围.分析 利用待定系数法列方程组即可求得k和b的值,根据一次函数的性质即可确定当x≥0时y的范围.
解答 解:根据题意得:$\left\{\begin{array}{l}{-3k+b=0}\\{b=-4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-4}\end{array}\right.$,
则函数的解析式是y=-$\frac{4}{3}$x-4.
∵一次项系数k=-$\frac{4}{3}$<0,
∴当x≥0时y的取值范围是y≤-4.
点评 本题考查了待定系数法求函数的解析式,以及一次函数的性质,正确解方程组求得k和b的值是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
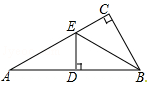 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于3cm.
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE+DE等于3cm.
 如图,AB是半圆O的直径,∠BAC=35°,则∠D的大小是125度.
如图,AB是半圆O的直径,∠BAC=35°,则∠D的大小是125度.