题目内容
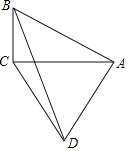
【题目】已知：如图所示，在
中，
、
分别是
和
的角平分线，交
、
于点
、
，连接
、
．
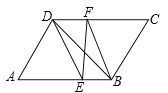
（1）求证：、互相平分；
（2）若
，
，
，求线段的长．
【答案】（1）证明见解析；（2）
【解析】
（1）证明四边形DEBF是平行四边形即可；
（2）过D点作DG⊥AB于点G，通过已知可证△ADE是等边三角形，所以GE=2，DE=4，由勾股定理可求DG=
，由
，得EB=2，所以GB=4，由勾股定理得
．
解：（1）证明：∵四边形ABCD是平行四边形，
∴CD∥AB，CD=AB，AD=BC，
∵DE、BF分别是∠ADC和∠ABC的角平分线，
∴∠ADE=∠CDE，∠CBF=∠ABF，
∵CD∥AB，
∴∠AED=∠CDE，∠CFB=∠ABF，
∴∠AED=∠ADE，∠CFB=∠CBF，
∴AE=AD，CF=CB，
∴AE=CF，
∴AB-AE=CD-CF 即BE=DF，
∵DF∥BE，
∴四边形DEBF是平行四边形，
∴BD、EF互相平分；
（2）过D点作DG⊥AB于点G，
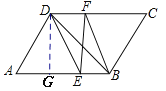
∵∠A=60°，AE=AD，
∴△ADE是等边三角形，
∵AD=4，
∴DE=AE=4，
∴
∵AE=2EB，
∴BE=2，
∴GB=4，
∴．
练习册系列答案
相关题目
【题目】某厂按用户需求生产一种产品，成本每件20万元，规定每件售价不低于成本，且不高于40万元。经市场调查，每年的销售量y（件）与每件售价x（万元）满足一次函数关系，部分数据如下表：
售价x（万元/件） | 25 | 30 | 35 |
销售量y（件） | 50 | 40 | 30 |
（1）求y与x之间的函数表达式；
（2）设商品每年的总利润为W（万元），求W与x之间的函数表达式（利润=收入-成本）；
（3）试说明（2）中总利润W随售价x的变化而变化的情况，并指出售价为多少万元时获得最大利润，最大利润是多少？
