题目内容
【题目】（阅读）：数学中，常对同一个量（图形的面积、点的个数、三角形的内角和等）用两种不同的方法计算，从而建立相等关系，我们把这一思想称为“算两次”．“算两次”也称做富比尼原理，是一种重要的数学思想．
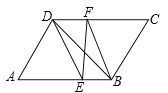
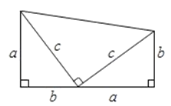
（理解）：（1）如图，两个边长分别为
、
、
的直角三角形和一个两条直角边都是的直角三角形拼成一个梯形．用两种不同的方法计算梯形的面积，并写出你发现的结论；
（2）如图2，
行列的棋子排成一个正方形，用两种不同的方法计算棋子的个数，可得等式：
________；
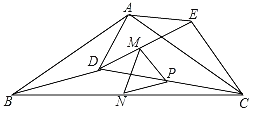
（运用）：（3）边形有个顶点，在它的内部再画
个点，以（
）个点为顶点，把边形剪成若干个三角形，设最多可以剪得
个这样的三角形．当
，
时，如图，最多可以剪得
个这样的三角形，所以
．
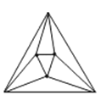
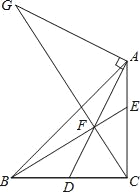
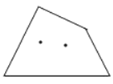
①当
，
时，如图，
；当
，
时，
；
②对于一般的情形，在边形内画个点，通过归纳猜想，可得 （用含、的代数式表示）．请对同一个量用算两次的方法说明你的猜想成立．
【答案】（1）见解析，故结论为：直角长分别为
、
斜边为
的直角三角形中
；（2）
；（3）①6，3；②
，见解析.
【解析】
（1）此等腰梯形的面积有三部分组成，利用等腰梯形的面积等于三个直角三角形的面积之和列出方程并整理．
（2）由图可知
行列的棋子排成一个正方形棋子个数为
，每层棋子分别为
，
，
，
，…，
．故可得用两种不同的方法计算棋子的个数，即可解答．
（3）根据探画出图形究不难发现，三角形内部每增加一个点，分割部分增加
部分，即可得出结论．
（1）有三个
其面积分别为
，和
．
直角梯形的面积为
．
由图形可知：
整理得
，
，
．
故结论为：直角长分别为、斜边为的直角三角形中．
（2）行列的棋子排成一个正方形棋子个数为，每层棋子分别为，，，，…，．
由图形可知：
．
故答案为：．
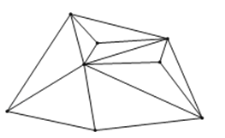
（3）①如图，当
，
时，
，
如图，当
，
时，
．
②方法1．对于一般的情形，在边形内画
个点，第一个点将多边形分成了个三角形，以后三角形
内部每增加一个点，分割部分增加部分，故可得
．
方法2．以
的二个顶点和它内部的个点，共（
）个点为顶点，可把分割成
个互不重叠的小三角形．以四边形的
个顶点和它内部的个点，共（
）个点为顶点，可把四边形分割成
个互不重叠的小三角形．故以边形的个顶点和它内部的个点，共（
）个点作为顶点，可把原n边形分割成个互不重叠的小三角形．故可得．
故答案为：①
，；②．
