题目内容
2.如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(-1,0)、B(4,0)两点,与y轴交于点C,且OC=3OA.点P是抛物线上的一个动点,过点P作PE⊥x轴于点E,交直线BC于点D,连接PC.(1)求抛物线的解析式;
(2)如图2,当动点P只在第一象限的抛物线上运动时,求过点P作PF⊥BC于点F,试问△PDF的周长是否有最大值?如果有,请求出其最大值,如果没有,请说明理由.
(3)当点P在抛物线上运动时,将△CPD沿直线CP翻折,点D的对应点为点Q,试问,四边形CDPQ是否成为菱形?如果能,请求出此时点P的坐标,如果不能,请说明理由.
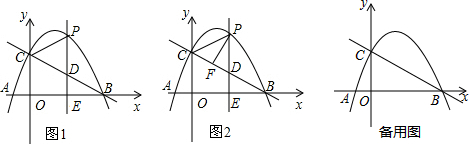
分析 (1)利用待定系数法求二次函数的解析式;
(2)设P(m,-$\frac{3}{4}$m2+$\frac{9}{4}$m+3),△PFD的周长为L,再利用待定系数法求直线BC的解析式为:y=-$\frac{3}{4}$x+3,表示PD=-$\frac{3}{4}{m}^{2}+3m$,证明△PFD∽△BOC,根据周长比等于对应边的比得:$\frac{△PFD的周长}{△BOC的周长}=\frac{PD}{BC}$,代入得:L=-$\frac{9}{5}$(m-2)2+$\frac{36}{5}$,求L的最大值即可;
(3)如图3,当点Q落在y轴上时,四边形CDPQ是菱形,根据翻折的性质知:CD=CQ,PQ=PD,∠PCQ=∠PCD,又知Q落在y轴上时,则CQ∥PD,由四边相等:CD=DP=PQ=QC,得四边形CDPQ是菱形,表示P(n,-$\frac{3}{4}{n}^{2}$+$\frac{9}{4}$n+3),则D(n,-$\frac{3}{4}$n+3),G(0,-$\frac{3}{4}n+3$),利用勾股定理表示PD和CD的长并列式可得结论.
解答 解:(1)由OC=3OA,有C(0,3),
将A(-1,0),B(4,0),C(0,3)代入y=ax2+bx+c中,得:
$\left\{\begin{array}{l}{a-b+c=0}\\{16a+4b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{3}{4}}\\{b=\frac{9}{4}}\\{c=3}\end{array}\right.$,
故抛物线的解析式为:y=-$\frac{3}{4}{x}^{2}$+$\frac{9}{4}$x+3;
(2)如图2,设P(m,-$\frac{3}{4}$m2+$\frac{9}{4}$m+3),△PFD的周长为L,
∵直线BC经过B(4,0),C(0,3),
设直线BC的解析式为:y=kx+b,
则$\left\{\begin{array}{l}{4k+b=0}\\{b=3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-\frac{3}{4}}\\{b=3}\end{array}\right.$
∴直线BC的解析式为:y=-$\frac{3}{4}$x+3,
则D(m,-$\frac{3}{4}m+3$),PD=-$\frac{3}{4}{m}^{2}+3m$,
∵PE⊥x轴,PE∥OC,
∴∠BDE=∠BCO,
∵∠BDE=∠PDF,
∴∠PDF=∠BCO,
∵∠PFD=∠BOC=90°,
∴△PFD∽△BOC,
∴$\frac{△PFD的周长}{△BOC的周长}=\frac{PD}{BC}$,
由(1)得:OC=3,OB=4,BC=5,
故△BOC的周长=12,
∴$\frac{L}{12}=\frac{-\frac{3}{4}{m}^{2}+3m}{5}$,
即L=-$\frac{9}{5}$(m-2)2+$\frac{36}{5}$,
∴当m=2时,L最大=$\frac{36}{5}$;
(3)存在这样的Q点,使得四边形CDPQ是菱形,如图3,
当点Q落在y轴上时,四边形CDPQ是菱形,
理由是:由轴对称的性质知:CD=CQ,PQ=PD,∠PCQ=∠PCD,
当点Q落在y轴上时,CQ∥PD,
∴∠PCQ=∠CPD,
∴∠PCD=∠CPD,
∴CD=PD,
∴CD=DP=PQ=QC,
∴四边形CDPQ是菱形,
过D作DG⊥y轴于点G,
设P(n,-$\frac{3}{4}{n}^{2}$+$\frac{9}{4}$n+3),则D(n,-$\frac{3}{4}$n+3),G(0,-$\frac{3}{4}n+3$),
在Rt△CGD中,CD2=CG2+GD2=[(-$\frac{3}{4}$n+3)-3]2+n2=$\frac{25}{16}{n}^{2}$,
而|PD|=|(-$\frac{3}{4}{n}^{2}+\frac{9}{4}n+3$)-(-$\frac{3}{4}$n+3)|=|-$\frac{3}{4}{n}^{2}$+3n|,
∵PD=CD,
∴-$\frac{3}{4}{n}^{2}+3n=\frac{5}{4}n$①,
-$\frac{3}{4}{n}^{2}+3n=-\frac{5}{4}n②$,
解方程①得:n=$\frac{7}{3}$或0(不符合条件,舍去),
解方程②得:n=$\frac{17}{3}$或0(不符合条件,舍去),
当n=$\frac{7}{3}$时,P($\frac{7}{3}$,$\frac{25}{6}$),如图3,
当n=$\frac{17}{3}$时,P($\frac{17}{3}$,-$\frac{25}{3}$),如图4,
综上所述,存在这样的Q点,使得四边形CDPQ是菱形,此时点P的坐标为($\frac{7}{3}$,$\frac{25}{6}$)或($\frac{17}{3}$,-$\frac{25}{3}$).
点评 本题是二次函数的综合题,考查了利用待定系数法求函数的解析式、菱形的性质和判定、三角形相似的性质和判定,将周长的最值问题转化为二次函数的最值问题,此类问题要熟练掌握利用解析式表示线段的长,并利用相似比或勾股定理列方程解决问题.

| A. | 3.14159是一个无理数 | B. | $\sqrt{0.25}$=±0.5 | ||
| C. | 若a为实数,则a2≥0 | D. | 16的平方根是4 |
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(2)产量最多的一天比产量最少的一天多生产27 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制.如果每生产一辆自行车就可以得人民币60元,超额完成任务,每超一辆可多得15元;若不足计划数的,每少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
| A. | 方程-2x+6=8,移项得-2x=8+6 | |
| B. | 方程3+$\frac{8}{9}$x=6-3(x-1),去括号得:3+$\frac{8}{9}$x=6-3x-1 | |
| C. | 不等式$\frac{3x-1}{5}$-1>0,去分母得:3x-1-5>0 | |
| D. | 不等式-$\frac{1}{2}$x≥3,解得:x≥-6 |
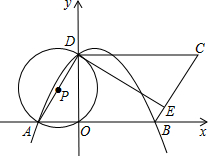 如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.
如图,在平面直角坐标系xoy中,O为原点,?ABCD的边AB在x轴上,点D在y轴上,点A的坐标为(-2,0),AB=6,∠BAD=60°,点E是BC边上一点,CE=3EB,⊙P过A、O、D三点,抛物线y=ax2+bx+c过点A、B、D三点.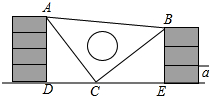 课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图所示.
课间,小明拿着老师的等腰直角三角板玩,不小心掉到两墙之间,如图所示.