题目内容
已知A、B在数轴上对应的数分别用a、b 表示,且( ab+100)2+|a﹣20|=0.P是数轴上的一个动点
ab+100)2+|a﹣20|=0.P是数轴上的一个动点
(1)在数轴上标出A、B的位置,并求出A、B之间的距离;
(2)数轴上一点C距A点24个单位长度,其对应的数c满足|ac|=﹣ac.当P点满足PB=2PC时,求P点对应的数;
(3)动点P从原点开始第一次向左移动1个单位长度,第二次向右移动3个单位长度,第三次向左移动5个单位长度第四次向右移动7个单位长度,….点P移动到与A或B重合的位置吗?若能,请探究第几次移动是重合;若不能,请说明理由.
【考点】数轴;绝对值.
【专题】规律型.
【分析】(1)根据平方与绝对值的和为0,可得平方与绝对值同时为0,可得a、b的值,根据两点间的距离,可得答案;
(2)根据根据两点间的距离公式,可得答案;
(3)根据观察,可发现规律,根据规律,可得答案.
【解答】解:(1)a=20,b=﹣10,AB=|20﹣(﹣10)|=30;
(2)∵|ac|=﹣ac,a=20>0,
∴c<0,又AC=24,
∴c=﹣4.
BC=6.
①P在BC之间时,点P表示﹣6,
②P在C点右边时,点P表示2;
(3)第一次点P表示﹣1,第二次点P表示2,依次﹣3,4,﹣5,6…则第n次为(﹣1)n•n,
d点A表示20,则第20次P与A重合;点B表示﹣10,点P与点B不重合.
【点评】本题考查了绝对值,两点间距离公式是解题关键,(2)要分类讨论,以防漏掉;(3)规律是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

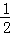 x+1=0
x+1=0

 的相反数是( )
的相反数是( )
 B.2 C.﹣2 D.
B.2 C.﹣2 D.
 .
.