题目内容
 如图,BCEF是平行四边形,△ABC是直角三角形BC长8cm,AC长7cm,阴影部分面积比△ADH的面积大12cm2.求AH的长.
如图,BCEF是平行四边形,△ABC是直角三角形BC长8cm,AC长7cm,阴影部分面积比△ADH的面积大12cm2.求AH的长.考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:根据平行线分线段成比例定理得出
=
,即可求得DH=
x,根据S四边形BCEF+S△ADH-S△ABC=S阴影列出方程,解方程即可求得AH的长.
| AH |
| AC |
| DH |
| BC |
| 8 |
| 7 |
解答:解:∵BC∥EF,AC⊥BC,
∴AC⊥EF,
∴
=
,
设AH=x,
∴
=
,
∴DH=
x,
∵S四边形BCEF+S△ADH-S△ABC=S阴影,
∴8(7-x)+
x•
x-
×7×8=
x•
x+12,解得:x=2,
即AH=2;
∴AC⊥EF,
∴
| AH |
| AC |
| DH |
| BC |
设AH=x,
∴
| x |
| 7 |
| DH |
| 8 |
∴DH=
| 8 |
| 7 |
∵S四边形BCEF+S△ADH-S△ABC=S阴影,
∴8(7-x)+
| 1 |
| 2 |
| 8 |
| 7 |
| 1 |
| 2 |
| 1 |
| 2 |
| 8 |
| 7 |
即AH=2;
点评:本题考查了平行四边形的性质,平行线分线段成比例定理的应用,根据题意列出方程是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
 如图可以拼成的几何体是( )
如图可以拼成的几何体是( )| A、三梭柱 | B、四棱柱 |
| C、圆柱 | D、圆锥 |
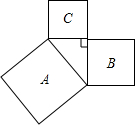 如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )
如图,正方形A、C的面积分别为169,25,则B所代表的正方形的边长为( )| A、12 | B、13 | C、144 | D、19 |
 如图,∠AOD=115°,OB是∠AOC的平分线,∠COD=27°,则∠BOD的度数为( )
如图,∠AOD=115°,OB是∠AOC的平分线,∠COD=27°,则∠BOD的度数为( )| A、88° | B、71° |
| C、44° | D、72° |
 如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数.
如图,CD是⊙O的直径,E是⊙O上一点,∠EOD=48°,A为DC延长线上一点,且AB=OC,求∠A的度数. 若AB∥CD,∠B、∠E、∠E、∠D三者满足关系
若AB∥CD,∠B、∠E、∠E、∠D三者满足关系