题目内容
13．已知关于x的方程（m-1）x2+3x+2=0有两个实数根，求正整数m的值．分析 根据方程（m-1）x2+3x+2=0有两个实数根可得m-1≠0，△=32-4×（m-1）×2≥0，解不等式求得m的范围即可得答案．
解答 解：∵关于x的方程（m-1）x2+3x+2=0有两个实数根，
∴m-1≠0，△=32-4×（m-1）×2≥0，
解得：m≤$\frac{17}{8}$且m≠1，
∴正整数m的值为2．
点评 本题主要考查根的判别式与一元二次方程的定义，一元二次方程ax2+bx+c=0（a≠0）的根与△=b2-4ac有如下关系：①当△＞0时，方程有两个不相等的两个实数根；②当△=0时，方程有两个相等的两个实数根；③当△＜0时，方程无实数根．
练习册系列答案
开心蛙口算题卡系列答案
相关题目
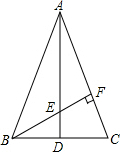如图，在△ABC中，AB=AC，点D是BC的中点，BF⊥AC于点F，交AD于点E，∠BAC=45°．求证：△AEF≌△BCF．
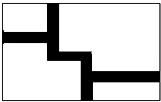如图，在长为32 米，宽为20 米的矩形地面上修建同样宽度的道路（图中阴影部分），余下的部分种植草坪，要使草坪的面积为540m2，求道路的宽是多少米？