题目内容
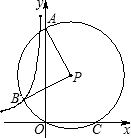 如图,⊙P过O、A(0,6)、C(2,0),半径PB⊥PA,双曲线
如图,⊙P过O、A(0,6)、C(2,0),半径PB⊥PA,双曲线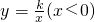 恰好经过B点,则k的值是________.
恰好经过B点,则k的值是________.
-4
分析:结合已知,设B的坐标为(x, )可根据点O、A、C的坐标得出圆心P的坐标,和PA的长,便可得出圆P所在的圆的方程;同时可得出直线PA的斜率,再根据两直线的垂直的斜率关系,可得出直线PB的斜率,利用两点确定直线的斜率,两方程联立即可得出k的值;
)可根据点O、A、C的坐标得出圆心P的坐标,和PA的长,便可得出圆P所在的圆的方程;同时可得出直线PA的斜率,再根据两直线的垂直的斜率关系,可得出直线PB的斜率,利用两点确定直线的斜率,两方程联立即可得出k的值;
解答:设B(x, ),结合题意,
),结合题意,
O(0,0)、A(0,6)、C(2,0),
即P(1,3),
所以PA= ,
,
故圆P:(x-1)2+(y-3)2=10;①
又∵直线PA的斜率为-3;
故直线PB的斜率为 ;
;
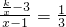 ;②
;②
联立①②,
可得k=-4.
故答案为:-4.
点评:本题主要考查了反比例函数的综合应用和圆的方程的应用,注意两直线垂直,斜率互为负倒数.
分析:结合已知,设B的坐标为(x,
 )可根据点O、A、C的坐标得出圆心P的坐标,和PA的长,便可得出圆P所在的圆的方程;同时可得出直线PA的斜率,再根据两直线的垂直的斜率关系,可得出直线PB的斜率,利用两点确定直线的斜率,两方程联立即可得出k的值;
)可根据点O、A、C的坐标得出圆心P的坐标,和PA的长,便可得出圆P所在的圆的方程;同时可得出直线PA的斜率,再根据两直线的垂直的斜率关系,可得出直线PB的斜率,利用两点确定直线的斜率,两方程联立即可得出k的值;解答:设B(x,
 ),结合题意,
),结合题意,O(0,0)、A(0,6)、C(2,0),
即P(1,3),
所以PA=
 ,
,故圆P:(x-1)2+(y-3)2=10;①
又∵直线PA的斜率为-3;
故直线PB的斜率为
 ;
;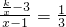 ;②
;②联立①②,
可得k=-4.
故答案为:-4.
点评:本题主要考查了反比例函数的综合应用和圆的方程的应用,注意两直线垂直,斜率互为负倒数.

练习册系列答案
相关题目

 (1)解方程:
(1)解方程: 如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=2,BC=6,则⊙O的半径为( )
如图,⊙O过点B、C.圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=2,BC=6,则⊙O的半径为( )
 如图,若过点P1,P2作直线m的平行线,则∠1、∠2、∠3、∠4间的数量关系是
如图,若过点P1,P2作直线m的平行线,则∠1、∠2、∠3、∠4间的数量关系是