题目内容
11. 如图,在正方形ABCD中,E是BC的中点,F是DC上的中点,且FC=$\frac{1}{4}$CD,试判断AE与EF的关系,并说明理由.
如图,在正方形ABCD中,E是BC的中点,F是DC上的中点,且FC=$\frac{1}{4}$CD,试判断AE与EF的关系,并说明理由.
分析 连接AF,设FC=a,分别计算AF,EF,AE的值,根据三角形三边长和勾股定理的逆定理可以判定△AEF为直角三角形,即可证明AE⊥EF.
解答 证明:连接AF,
设FC=a,则DC=DA=AB=BC=4
所以DF=3a,CE=EB=2a.
由勾股定理得AF=5a,
EF=$\sqrt{5}$a,AE=2$\sqrt{5}$a从而由
($\sqrt{5}$a)2+(2$\sqrt{5}$)2=(5a)2
即EF2+AE2=AF2
∴△AEF为直角三角形,斜边为AF,
故∠AEF=90°,
即AE⊥EF.
点评 本题考查了勾股定理在直角三角形中的运用,考查了正方形各边长相等、各内角为直角的性质,考查了勾股定理的逆定理判定直角三角形的方法,本题中判定△AEF为直角三角形是解题的关键.

练习册系列答案
相关题目
2.某市客运管理部门对“十一”国庆假期七天客流变化量进行了不完全统计,数据如下(用正数表示客流量比前一天上升数,用负数表示比前一天下降数).
与9月30日相比,10月7日的客流量是上升了还是下降了?变化了多少?
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 变化/万人 | 20 | -3 | -10 | -3 | 2 | 9 | 3 |
19.已知a<b,则下列式子正确的是( )
| A. | a-3>b-3 | B. | a+1>b+1 | C. | 2a>2b | D. | -5a>-5b |
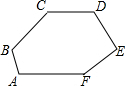 如图,已知在六边形ABCDEF中,CD∥AF,∠D=∠A,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.(提示:延长CB与FA的延长线交于点G)
如图,已知在六边形ABCDEF中,CD∥AF,∠D=∠A,AB⊥BC,∠C=124°,∠E=80°,求∠F的度数.(提示:延长CB与FA的延长线交于点G)