题目内容
17.a,b,c,d均不为0,a≠b时,$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{d}$=$\frac{d}{a}$,求$\frac{a+b+c+d}{b+c+d-a}$.分析 设$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{d}$=$\frac{d}{a}$=k,计算出k的值,代入所求的式子计算得到答案.
解答 解:设$\frac{a}{b}$=$\frac{b}{c}$=$\frac{c}{d}$=$\frac{d}{a}$=k,
则a=bk,b=ck,c=dk,d=ak,
整理得,a=ak4,
解得,k1=1(舍去),k2=-1,
即a=-b,c=-d,
则$\frac{a+b+c+d}{b+c+d-a}$=0.
点评 本题考查的是比例的性质,根据题意设出比值、计算出比值是解题的关键.

练习册系列答案
相关题目
10.计算(-3)×2-1的结果是( )
| A. | -5 | B. | -7 | C. | 6 | D. | -6 |
5.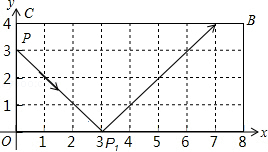 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P2015的坐标是( )| A. | (1,4) | B. | (3,0) | C. | (7,4) | D. | (5,0) |
9.若M(1-3x2)=1-9x4,则M等于( )
| A. | 1-3x2 | B. | (1-3x2)2 | C. | 1+3x2 | D. | (1+3x2)2 |