题目内容
7.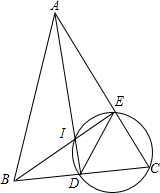 如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=$\frac{\sqrt{3}}{3}$.
如图,若AD、BE为△ABC的两条角平分线,I为内心,若C,D,I,E四点共圆,且DE=1,则ID=$\frac{\sqrt{3}}{3}$.
分析 由已知条件和三角形的内角和定理可求出∠ACB=60°,再由I为内心即可得到∠ICD=30°,由正弦定理即可求出ID的长.
解答 解:连接CI,
∵AD、BE为△ABC的两条角平分线,
∴∠BAI=$\frac{1}{2}$∠BAC,∠IBA=$\frac{1}{2}$∠ABC,
∵∠AIB=180°-∠BAI-∠IBA,
∴∠AIB=180°-$\frac{1}{2}$(∠CAB+∠CBA),
又∵∠ABC+∠CBA+∠ACB=180°,
∴∠AIB=90°+$\frac{1}{2}$∠C,
∵C,D,I,E四点共圆,
∴∠EID+∠ACB=180°,
又∵∠AIB=∠EID,
∴90°+$\frac{1}{2}$∠C+∠C=180°,
∴∠ACB=60°,
∵I为内心,
∴∠ICD=30°,
∵DE=1,
∴$\frac{DE}{sin60°}$=2R,
∴R=$\frac{\sqrt{3}}{3}$,
∴$\frac{ID}{sin30°}=2R$,
∴ID=$\frac{\sqrt{3}}{3}$,
故答案为:$\frac{\sqrt{3}}{3}$.
点评 本题考查了三角形内接圆的性质、三角形内接四边形的性质以及正弦定理的运用,题目的综合性较强有一定的难度,求出∠C的度数是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
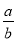 =
=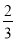 ,那么
,那么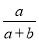 的值为( )
的值为( )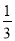 B.
B. 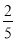 C.
C. 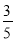 D.
D. 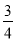
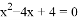 的根的情况是 ( )
的根的情况是 ( )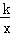 (x>0)的图象经过点M(1,﹣1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=______.
(x>0)的图象经过点M(1,﹣1),过点M作MN⊥x轴,垂足为N,在x轴的正半轴上取一点P(t,0),过点P作直线OM的垂线l.若点N关于直线l的对称点在此反比例函数的图象上,则t=______.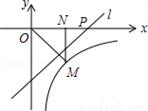
 如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.
如图,将一张矩形纸片ABCD沿直线MN折叠,使点C落在点A处,点D落在点E处,直线MN交BC于点M,交AD于点N.