题目内容
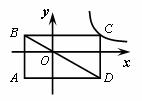
如图1,在平面直角坐标系xOy中,等腰直角△AOB的斜边OB在x上,顶点A的坐标为(3,3).
(1)求直线OA的解析式;
(2)如图2,如果点P是x轴正半轴上的一个动点,过点P作PC∥y轴,交直线OA于点C,设点P的坐标为(m,0),以A、C、P、B为顶点的四边形面积为S,求S与m之间的函数关系式;
(3)如图3,如果点D(2,a)在直线AB上. 过点O、D作直线OD,交直线PC于点E,在CE的右侧作矩形CGFE,其中CG=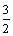 ,请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
,请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.

图1 图2 图3
解:(1)设直线OA的解析式为y=kx.
∵直线OA经过点A(3,3),
∴3=3k,解得 k=1.
∴直线OA的解析式为y=x. ………………………………………………2分
(2)过点A作AM⊥x轴于点M.
∴M(3,0),B(6,0),P(m,0),C(m,m).
当0<m<3时,如图1.
S=S△AOB-S△COP
=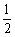 AD·OB-
AD·OB-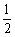 OP·PC
OP·PC
=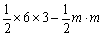 =
=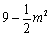 .………………………………………………4分
.………………………………………………4分
当3<m<6时,如图2.
S=S△COB-S△AOP
=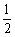 PC·OB-
PC·OB-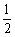 OP·AD
OP·AD
=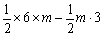 =
=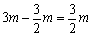 .……………………………………5分
.……………………………………5分
当m>6时,如图3.
S=S△COP-S△AOB
=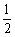 PC·OP-
PC·OP-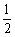 OB·AD
OB·AD
=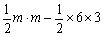
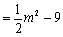 .…………………………………………6分
.…………………………………………6分
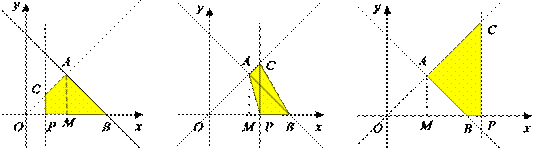
图1 图2 图3
(3)m的取值范围是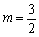 ,
,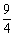 ≤m<3. ……………………………………8分
≤m<3. ……………………………………8分

练习册系列答案
相关题目
 D作OD⊥OC,OD与
D作OD⊥OC,OD与
 当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.
当点C在⊙O上运动到什么位置时,△ABC的面积最大?并求出△ABC的面积的最大值.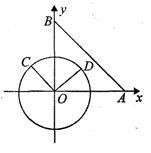

 ,D是BC的中点,
,D是BC的中点,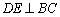 ,CE∥AD.如果AC=2,CE=4.
,CE∥AD.如果AC=2,CE=4.
 ,当
,当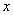 的值减小1,
的值减小1, 的值就减小2,则当
的值就减小2,则当 = .
= . BE=CF,AF=DE.
BE=CF,AF=DE.
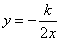 的图象上,若点A的坐标为 (-2,-2),则k的值为( )A.4 B.-4 C.8 D.—8
的图象上,若点A的坐标为 (-2,-2),则k的值为( )A.4 B.-4 C.8 D.—8