题目内容
已知:如图,在△ABC中,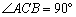 ,D是BC的中点,
,D是BC的中点,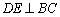 ,CE∥AD.如果AC=2,CE=4.
,CE∥AD.如果AC=2,CE=4.
(1)求证:四边形ACED是平行四边形;
(2)求四边形ACEB的周长;
(3)直接写出CE和AD之间的距离.

(1)证明:∵∠ACB=90°,DE⊥BC,∴AC∥DE. ……………………………1分
 又∵CE∥AD,
又∵CE∥AD,
∴四边形ACED是平行四边形. ………2分
(2)解:∵四边形ACED的是平行四边形.
∴DE=AC=2.
在Rt△CDE中,∵∠CDE=90°,
由勾股定理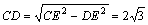 .……………………………………3分
.……………………………………3分
∵D是BC的中点,
∴BC=2CD=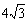 .
.
在Rt△ABC中,∵∠ACB=90°,
由勾股定理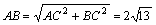 .…………………………………4分
.…………………………………4分
∵D是BC的中点,DE⊥BC,
∴EB=EC=4.
∴四边形ACEB的周长= AC+CE+EB+BA=10+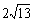 .…………………5分
.…………………5分
(3)解:CE和AD之间的距离是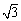 .……………………………………………6分
.……………………………………………6分

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 初中毕业生总数将达到52500人,这个数据用科学计数法可表示为 .
初中毕业生总数将达到52500人,这个数据用科学计数法可表示为 .
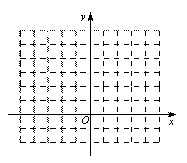
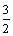 ,请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
,请你直接写出矩形CGFE与△AOB重叠部分为轴对称图形时m的取值范围.
