题目内容
如图(1),抛物线 与x轴交于A、B两点,与y轴交于点C(0,
与x轴交于A、B两点,与y轴交于点C(0, ).[图(2)为解答备用图]
).[图(2)为解答备用图]

(1) __________,点A的坐标为___________,点B的坐标为__________;
__________,点A的坐标为___________,点B的坐标为__________;
(2)设抛物线 的顶点为M,求四边形ABMC的面积;
的顶点为M,求四边形ABMC的面积;
(3)在x轴下方的抛物线上是否存在一点D,使四边形ABDC的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.
(1) k=-3,A(-1,0),B(3,0);(2)9;(3) 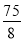 .
.
【解析】
试题分析:(1)将C点坐标代入抛物线的解析式中,即可求出k的值;令抛物线的解析式中y=0,即可求出A、B的坐标;
(2)将抛物线的解析式化为顶点式,即可求出M点的坐标;由于四边形ACMB不规则,可连接OM,将四边形ACMB的面积转化为△ACO、△MOC以及△MOB的面积和;
(3)当D点位于第三象限时四边形ABCD的最大面积显然要小于当D位于第四象限时四边形ABDC的最大面积,因此本题直接考虑点D为与第四象限时的情况即可;设出点D的横坐标,根据抛物线的解析式即可得到其纵坐标;可参照(2)题的方法求解,连接OD,分别表示出△ACO、△DOC以及△DOB的面积,它们的面积和即为四边形ABDC的面积,由此可得到关于四边形ABDC的面积与D点横坐标的函数关系式,根据函数的性质即可求出四边形ABDC的最大面积及对应的D点坐标.
试题解析:(1)由于点C在抛物线的图象上,则有:k=-3;
∴y=x2-2x-3;
令y=0,则x2-2x-3=0,
解得x=-1,x=3,
∴A(-1,0),B(3,0);
(2)抛物线的顶点为M(1,-4),连接OM;
则△AOC的面积=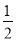 AO•OC=
AO•OC=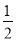 ×1×3=
×1×3=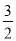 ,
,
△MOC的面积=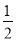 OC•|xM|=
OC•|xM|=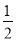 ×3×1=
×3×1=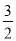 ,
,
△MOB的面积=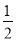 OB•|yM|=
OB•|yM|=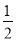 ×3×4=6;
×3×4=6;
∴四边形ABMC的面积=△AOC的面积+△MOC的面积+△MOB的面积=9;
(3)设D(m,m2-2m-3),连接OD;
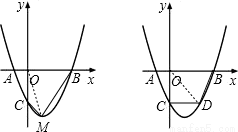
则0<m<3,m2-2m-3<0;
且△AOC的面积=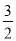 ,△DOC的面积=
,△DOC的面积=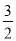 m,△DOB的面积=-
m,△DOB的面积=-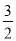 (m2-2m-3);
(m2-2m-3);
∴四边形ABDC的面积=△AOC的面积+△DOC的面积+△DOB的面积
=-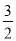 m2+
m2+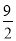 m+6=-
m+6=-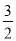 (m-
(m-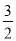 )2+
)2+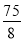 ;
;
∴存在点D(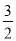 ,-
,-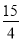 ),使四边形ABDC的面积最大,且最大值为
),使四边形ABDC的面积最大,且最大值为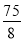 .
.
考点:二次函数综合题.


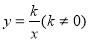 上的一点,则下列各点中不在该图象上的是( )
上的一点,则下列各点中不在该图象上的是( )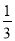 ,-15) B.(5,1) C.(-1,5) D.(10,
,-15) B.(5,1) C.(-1,5) D.(10, )
)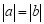 ,则a与b的关系是( )
,则a与b的关系是( )